基础
二次导数
二次导数代表了函数的平滑程度,$y''$越大则函数坡度越大,变化越大。
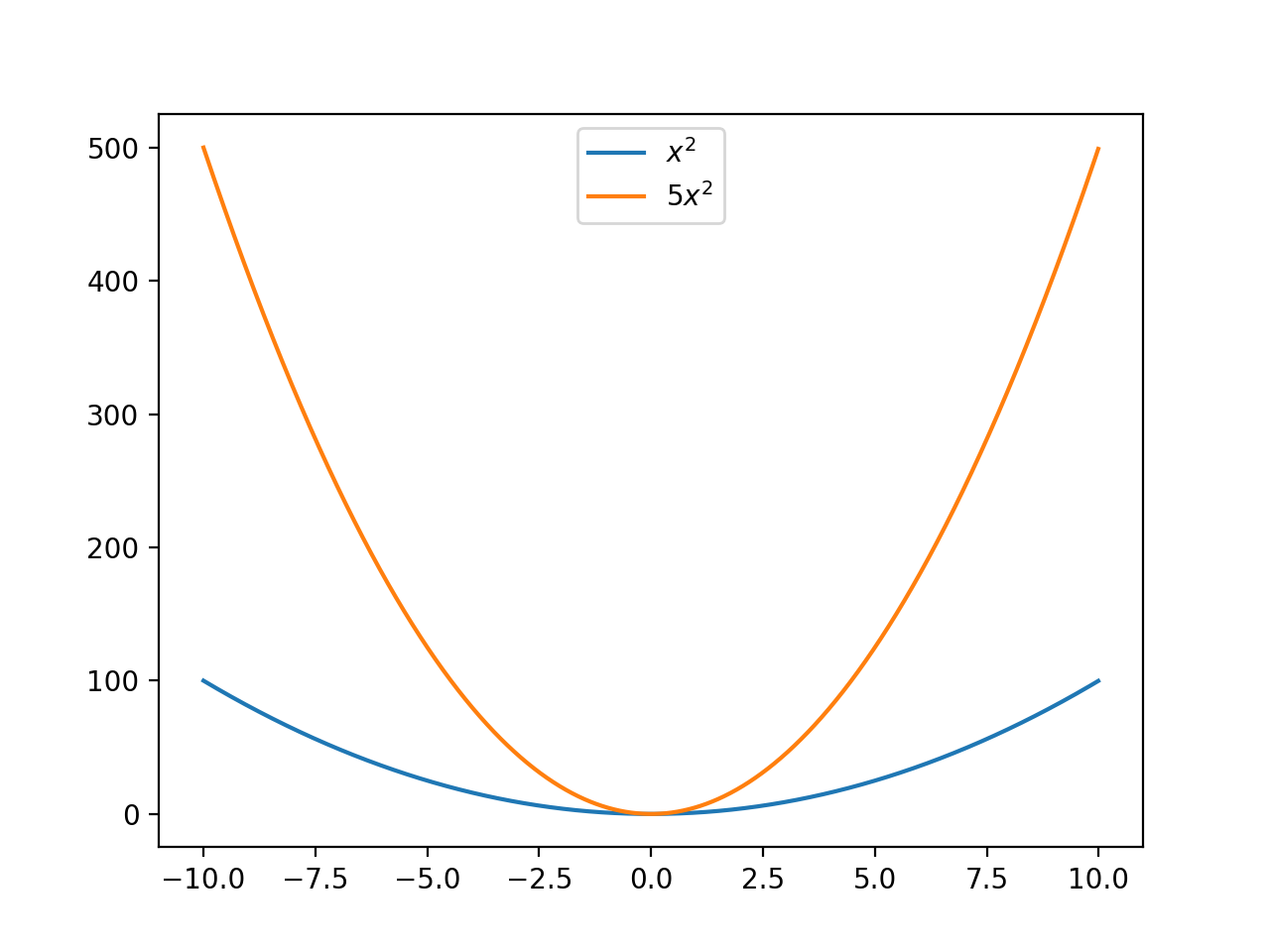
所以我们若是想要函数平滑一点,可以将二次导数添加到损失函数中去: $$ cost(f, \lambda) = \sum_{i=1}^N (y_i - f(x_i))^2 + \lambda \int [f''(x)]^2dx $$
基本定义
-
equivariance
一个函数是equivariance表示,我们对函数的输入进行一定的变化,函数的输出也保持这个变化
-
invariant
一个函数是invariant表示,我们对输入进行轻微的改变,输出保持不变。
-
symmetric
一个函数是symmetric,表示我们改变输入变量的位置输出保持不变即:$f(x_1, x_2, \cdot, x_n) = f(x_2, x_1, \cdots, x_n)$。比如函数f(x_1, x_2, x_3) = (x-x_1)(x-x_2)(x-x_3)