liudy

概率论笔记

本文记录概率论相关的笔记
 Study  2093  5 分钟  

基础

A和B为两个随机事件, $$ p(A \cup B) = p(A) + p(B) - p(A \cap B) $$ 如果A与B独立不相关(mutually exclusive) $$ p(A \cup B) = p(A) + p(B) $$

联合概率(joint probabilities) $$ p(A, B) = p(A \cap B) = p(A|B)p(B) $$ 如果A与B相互独立(marginally independent) $$ p(A, B) = p(A)p(B) $$

条件概率（Conditional probability） $$ p(A|B) = \frac{p(A, B)}{p(B)} \ if \ p(B) > 0 $$

贝叶斯定理(Bayes Theorem) $$ P(X=x|Y = y) = \frac{p(X=x, Y=y)}{p(Y=y)} = \frac{p(X=x)p(Y=y | X = x)}{\sum_{x'}p(X=x')p(Y=y | X=x')} $$ 其中$p(X=x)$称为先验概率，$P(X=x|Y=y)$称为后验概率。

条件独立

当下式满足时, 我们说$X$和$Y$关于$Z$条件独立(conditionally independent)： $$ X \perp Y | Z \Longleftrightarrow p(X, Y | Z) = p(X|Z)p(Y|Z) $$

定理:

$X \perp Y | Z$ 当且仅当存在函数$g$核函数$h$使得： $$ p(x, y|z) = g(x, z)h(y, z) $$ 对于任意$x,y,z$成立，$p(z) > 0$

期望与方差

期望（mean, expected value）: $$ E[X] = \sum_{x\in X} x p(x) $$ $$ E[X] = \int_{X} x p(x) dx $$

方差（variance）: $$ var[X] = E[(X - u)^2] = \int (x-u)^2 p(x) dx = E[X^2] - u^2 $$ 由此可得$E[X^2] = u^2 + \sigma^2$

标准差（standard deviation）定义为： $$ std[X] = \sqrt{var[X]} $$

协方差

协方差矩阵一定是半正定矩阵，证明如下：

对于任意多元随机变量$t$，协方差矩阵为： $$ C = \mathbb{E}[(t-\bar{t})(t - \bar{t})^T] $$ 对于给定的一个向量$x$，有：

$$ x^T C x = X^T \mathbb{E}[(t-\bar{t})(t-\bar{t})^T] x $$ $$ = \mathbb{E}[x^T(t-\bar{t})(t-\bar{t})^T x] $$ $$ = \mathbb{E}(s^2) = \sigma^2_s $$

其中， $$ \sigma_s = x^T(t-\bar{t}) = (t-\bar{t})^T x $$ 由于$\sigma_s^2 \geq 0$，因此$x^T C x \geq 0$, 所以协方差矩阵$C$是半正定的。

抽屉原理

  1. 把$n$个相同的球放进$k$个不同的盒子中的方案数

    可以看成是$n+k$个球放进$k$个盒子中，每个盒子至少有一个球,所以采用隔板法可得$C_{n+k-1}^{k-1}$

最小二乘法的最大似然估计解释

首先我们假设预测值和真实值之间的误差$e_i$f服从高斯分布$N(0, \sigma^2)$, 则$P(e_1, e_2, \cdots, e_n)$的概率为:

$$ \begin{array}{ll} p & = \frac{1}{\sqrt{2\pi}\sigma}\exp^{-\frac{e_1^2}{2\sigma^2}}\cdots \frac{1}{\sqrt{2\pi}\sigma}\exp^{-\frac{e_n^2}{2\sigma^2}} \\ & = \frac{1}{\sqrt{2\pi}\sigma}\exp^{-\frac{1}{2\sigma^2}\sum_{i=1}^n e_i^2} \end{array} $$

上式中我们要最大化似然概率，即等价于最小化$\sum_{i=1}^n e_i^2$（最小二乘法）

分布函数

伯努里分布(Bernoulli)

$$ \left\{ \begin{array}{rcl} Pr(X=1) &=& p \\ Pr(X=0) &=& 1 - p \end{array}\right. $$

Zipf分布

$$ f(x) = \frac{1}{x^\alpha \sum_{i=1}^n (1/i)^\alpha} \ \ \ x=1, 2, \cdots, n. $$ zipf分布适用于小部分成员出现的概率很高，而其他成员出现的概率低的情况。比如在图书馆中某几本书被借的概率很高，而其它大部分书很少被借。

下图展示了参数$\alpha=1$，$n=10$的zipf分布图

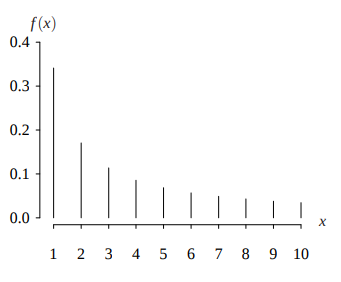
正态分布

单变量的正态分布表示为： $$ p(x) = \frac{1}{\sqrt{2\pi}\sigma}\exp^{-\frac{1}{2} (\frac{x-u}{\sigma})^2} $$ 其中，$x$为随即变量，$u$为$x$的期望，$\sigma$为$x$的标准差，$\sigma ^2$为$x$的方差,记作$N(u, \sigma^2)$

性质

  • 假设$x' = ax + b$，则$x'\sim N(au+b, a^2\sigma^2)$
  • 假设$x' = x + y$,且 $x \sim N(u_x, \sigma^2_x), y \sim N(u_y, \sigma^2_y)$, 则$x' \sim$ $N(u_x + u_y,$ $\sigma^2_x + \sigma_y^2)$

t分布(Student t distribution)

对于高斯分布有一个问题是它对于异常点敏感，如下图，在右侧有异常点对于高斯分布影响很大，而对t分布和laplace分布影响较小，原因是这两个分布都是重尾分布(heavy tails)。

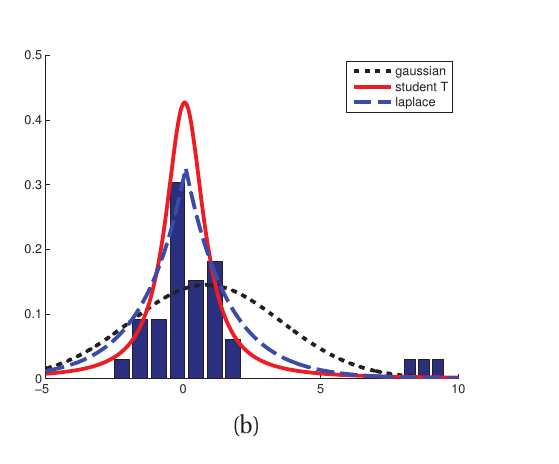
t分布的概率密度函数为： $$ \mathcal{T}(x | u, \sigma^2, v) \propto [1 + \frac{1}{v}(\frac{x-u}{\sigma})^2]^{-\frac{v+1}{2}} $$ 其中$u$为期望, $\sigma^2 > 0$ 是系数，$v>0$为自由度（degrees of freedom）。有以下性质： $$ mean = u, mode = u, var = \frac{v\sigma^2}{v-2} $$

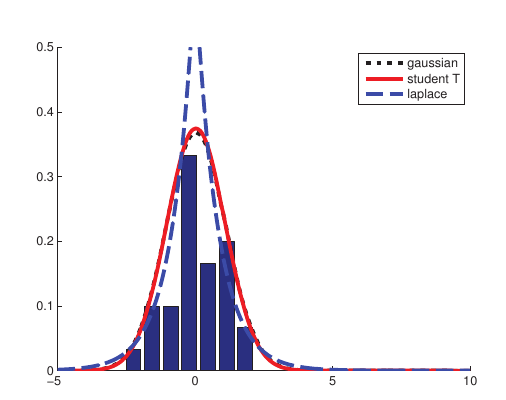为了保证拥有有限的方差，需要要求$v>2$。一般常用的是令$v=4$,该值在很多问题上都表现良好。当$v \gg 5$时该分布迅速的近似高斯分布。

拉普拉斯分布（Laplace）

拉普拉斯是另一个重尾(heavy tails)分布，也称为double sided exponential分布（如图两边都是一个指数分布）。其概率密度函数为： $$ Lap(x|u, b) \triangleq \frac{1}{2b} \exp(-\frac{|x-u|}{b}) $$ 该分布有性质： $$ mean=u, mode=u, var=2b^2 $$ 该分布对于异常点拥有很好的鲁棒性，在0处的概率密度大于高斯分布，该性质会驱使模型更加的稀疏。

Gamma 分布

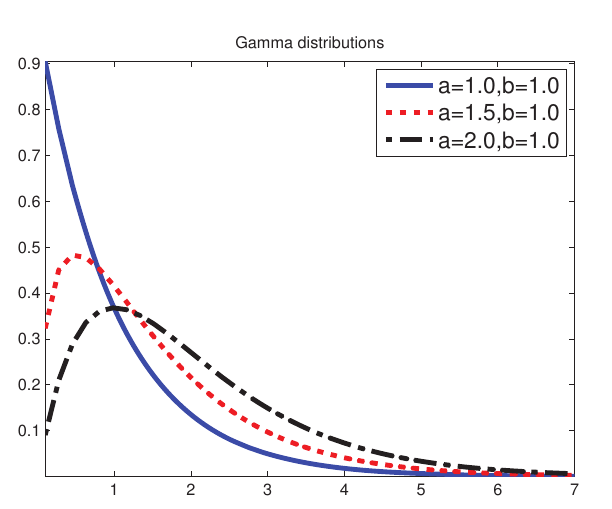Gamma 分布的概率密度函数为： $$ Ga(T | shape=a, rate = b) \triangleq \frac{b^a}{\Gamma(a)}T^{a-1}e^{-Tb} $$ 其中$\Gamma(a)$是gamma函数 $$ \Gamma(x) \triangleq \int_0^{\infty} u^{x-1} e^{-u} du $$ 该分布的性质： $$ mean = \frac{a}{b}, mode = \frac{a-1}{b}, var = \frac{a}{b^2} $$ 特殊的gamma分布：

  • 指数分布(exponential distribution):$Expon(x|\lambda) = \triangleq Ga(x| 1, \lambda)$
  • Erlang distribution: $Erlang(x|\lambda) = Ga(x|2, \lambda)$
  • Chi-squared distribution: $\mathcal{X}^2(x|v) \triangleq Ga(x| \frac{v}{2}, \frac{1}{2})$

gamma分布还有一个很有用的性质：如果$X \perp Ga(a, b)$则$\frac{1}{X} \perp IG(a, b)$,其中IG是inverse gamma 分布： $$ IG(x| shape=a, scale=b) \triangleq \frac{b^a}{\Gamma}x^{-(a+1)}e^{-b/x} $$ 其中该分布的性质为： $$ mean=\frac{b}{a-1}, mode = \frac{b}{a+1}, var=\frac{b^2}{(a-1)^2(a-2)} $$

伯努利分布(Bernoulli)

随机变量$x$只有两种值{0, 1},概率质量函数： $$ P(x) = p^x(1-p)^{1-x} $$

二项式分布（binomial）

$$ Bin(k | n, \theta) = C_n^k \theta^k (1 - \theta)^{n - k} $$ 期望$u = \theta$, 方差$var = n\theta(1-\theta)$

泊松分布（Poisson）

变量$X \in {0, 1, 2, \cdots}$， 参数$\lambda > 0$, 泊松分布$X \perp Poi(\lambda)$: $$ Poi(x | \lambda) = e^{-\lambda} \frac{\lambda^x}{x!} $$

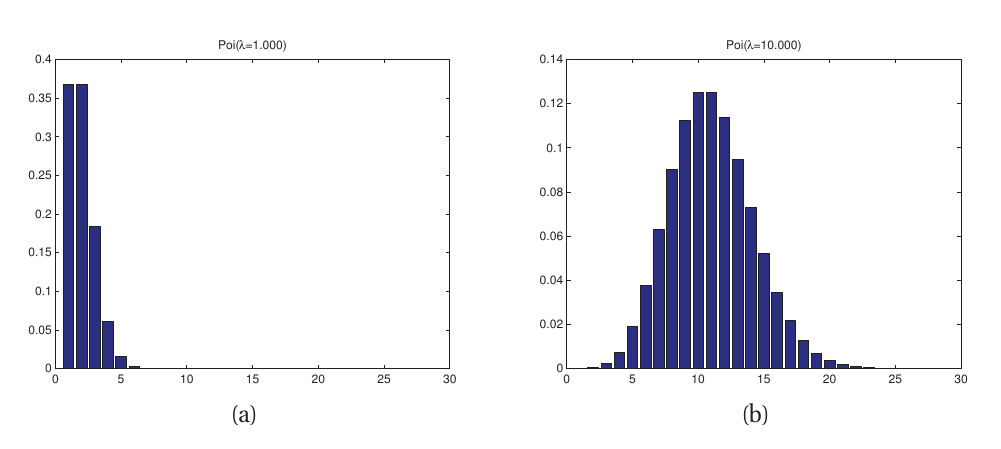
多维高斯分布

$$ p(x;u, \Sigma) = \frac{1}{(2\pi)^{n/2} |\Sigma|^{1/2}}\exp(- \frac{1}{2} (x-u)^T \Sigma^{-1} (x-u)). $$

高斯分布在机器学习和统计学上非常的有用在于两个方便：

  1. 使用高斯分布来模拟“noise”，因为根据中心极限定理，小的独立变量的和会趋向于高斯分布
  2. 高斯分布对于分析很方便，有很多简单的闭合形式的解（closed form solutions）

性质：

  1. 边缘分布（marginalization）也是高斯分布
  2. 条件概率分布（conditioning）也是高斯分布
  3. 高斯变量的和还是高斯分布

原分布为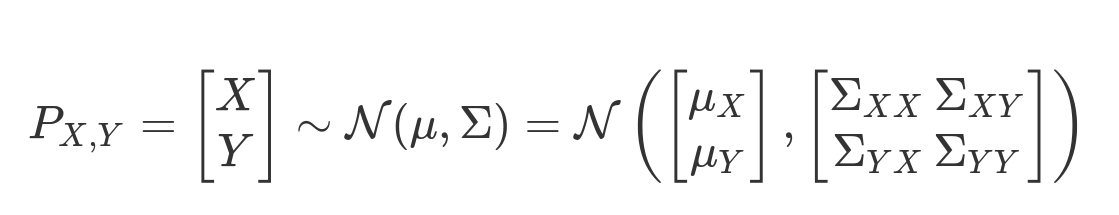： 边缘分布 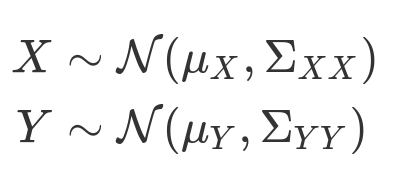条件概率分布：

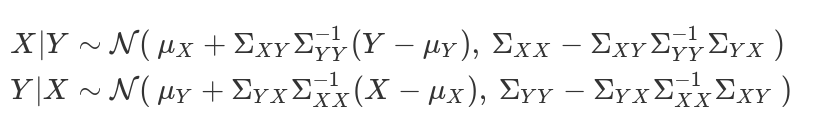
高斯变量的和 $$ \sum_{i=1}^n y_i \sim N(\sum_{i=1}^n u_i, \sum_{i=1}^n \sigma^2_i) $$

updatedupdated2021-11-062021-11-06

相关文章：