偏差和方差
数学定义
假定我们想要通过变量$X$,来预测$Y$的值。$\hat{f}(x)$为我们训练得到的模型,可知平方误差的期望为:
$$
\begin{array}{ll}
Err(x)& = E[(Y - \hat{f}(x))^2] \\
&= E[Y^2 - 2Y\hat{f}(x) + \hat{f}^2(x)] \\
&= Y^2 - 2YE[\hat{f}(x)] + E[\hat{f}^2(x)] \\
&= Y^2 - 2YE[\hat{f}(x)] + E^2[\hat{f}(x)] + E[\hat{f}^2(x)] - 2E^2[\hat{f}(x)] + E^2[\hat{f}(x)] \\
&= (Y - E[\hat{f}(x)])^2 + E[\hat{f}^2(x)] - 2E[E[\hat{f}(x)]\hat{f}(x)] + E^2[\hat{f}(x)] \\
&= (Y - E[\hat{f}(x)])^2 + E[(\hat{f}(x) - E[\hat{f}(x)])^2] \\
&= Bias^2 + Variance
\end{array}
$$
概念定义
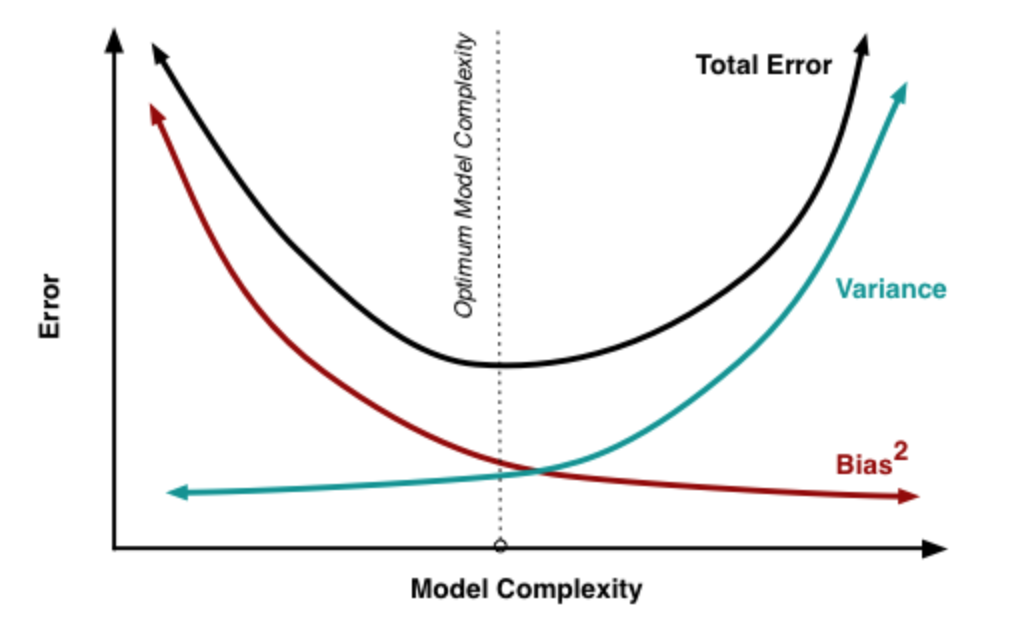
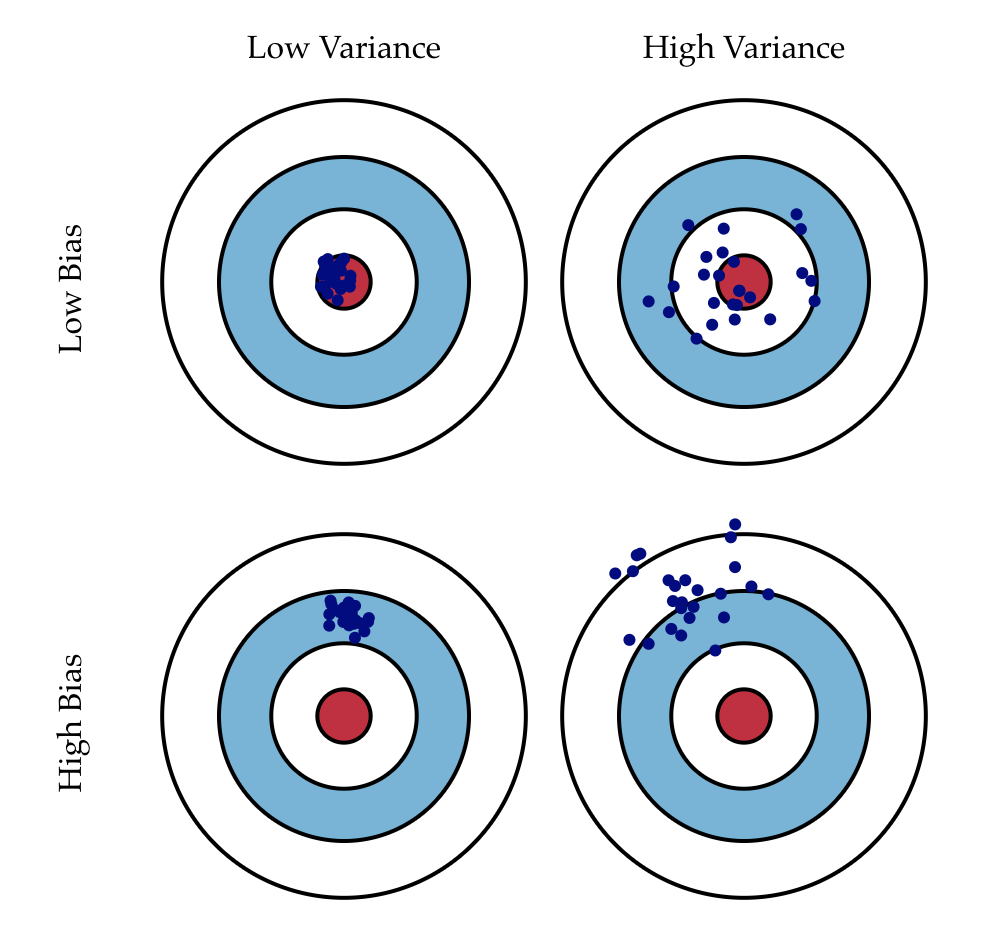
偏差: 反映的是我们预测的值和真实值之间误差的期望大小。此处期望是指假设我们重复整个模型训练过程获得许多的模型,再来得到误差的期望值。(此处的随机因素来源于训练数据的随机性),偏差代表了模型的拟合能力。
方差: 反映的是当你对一个模型使用不同的数据进行多次建模时,这些模型在某一个点上的预测值的方差。方差代表了算法的鲁棒性。
偏差与方差之间的平衡,反映了过拟合与欠拟合之间的平衡。随着模型越来越复杂,偏差会下降,方差会变大,如下图所示: