矩阵笔记

半正定（posivive semidefinite）

一个对称矩阵$A\in R^{n\times n}$ 是半正定矩阵，其要满足： $$ x^T A x \geq 0 \ for \ all \ x $$

正定（positive definite）

一个对称矩阵$A\in R^{n\times n}$ 是正定矩阵，其要满足： $$ x^T A x > 0 \ for \ all \ x \neq 0 $$

性质

所有的正定矩阵都是非奇异（nonsingular）的: $$ Ax = 0 \Rightarrow x^TAx=0 \Rightarrow x = 0 $$
所有的正定矩阵的对角元素都是正数： $$ A_{ii} = e_i^TAe_i > 0 $$
所有的半正定矩阵的对角元素都是非负数： $$ A_{ii} = e_i^TAe_i \geq 0 $$

Schur complement

将对称矩阵$A$进行分块为： $$ A = \left[ \begin{array}{cc} A_{11} & A^T_{2:n,1} \
A_{2:n,1} & A_{2:n,2:n}

\end{array} \right] $$

定义$A_{11}$的Schur complement为一个$(n-1)\times (n-1)$ 的矩阵： $$ S = A_{2:n,2:n} - \frac{1}{A_{11}}A_{2:n,1}A^T_{2:n,1} $$

如果$A$是正定，则$S$也是正定

Gram Matrix

定义： 矩阵$B$的Gram矩阵定义为： $$ A = B^TB $$

性质

所有的Gram矩阵都是半正定矩阵
如果矩阵$B$的列向量是线性独立的则Gram矩阵是正定的。

$$ x^TAx=x^TB^TBx=||Bx||^2 > 0 \ \forall x \neq 0 $$

Graph Laplacian

定义： 一个有向图的关联矩阵表示为：

$$ B_{i,j} = \left\{ \begin{array}{rl} 1 & 存在点j指向点i的有向边\\ -1 & 存在点i指向点j的有向边\\ 0 & otherwise \end{array} \right. $$

例子：

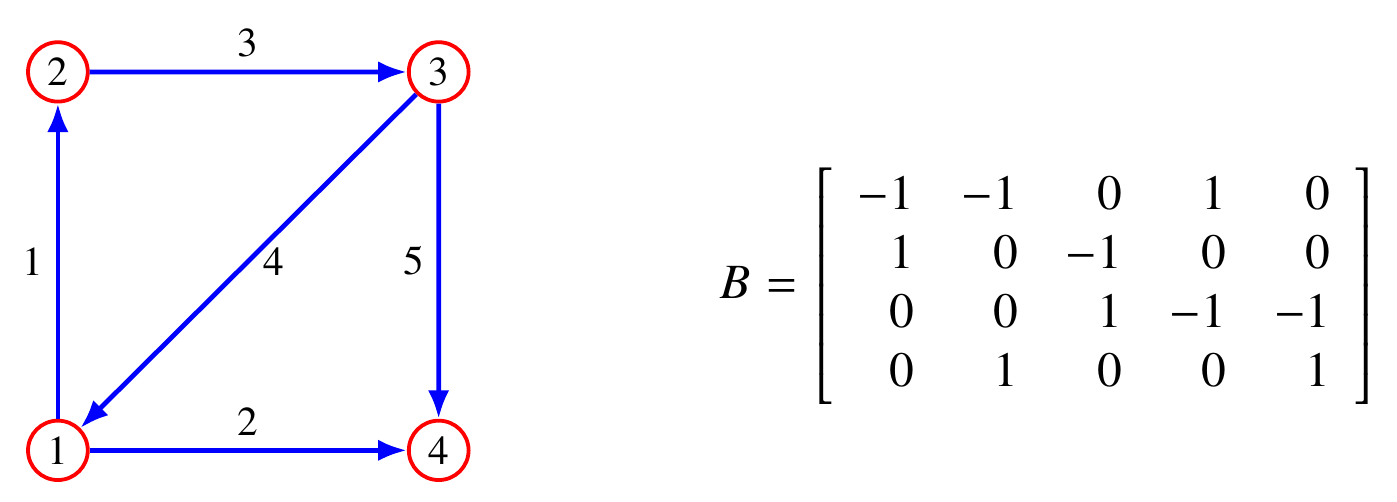
定义： 半正定矩阵$A=BB^T$为Laplacian of the graph

$$ A_{i,j}=\left\{ \begin{array}{ll} degree\ of\ node \ i & if\ i = j\\ -1 & if\ i \neq j \ and \ there \ is \ an \ arc \ i \rightarrow j\ or\ j \rightarrow i \\ 0 & otherwise \end{array} \right. $$

其中的degree of node i 包含了出度和入度（即和该点相关联的边数）

例子

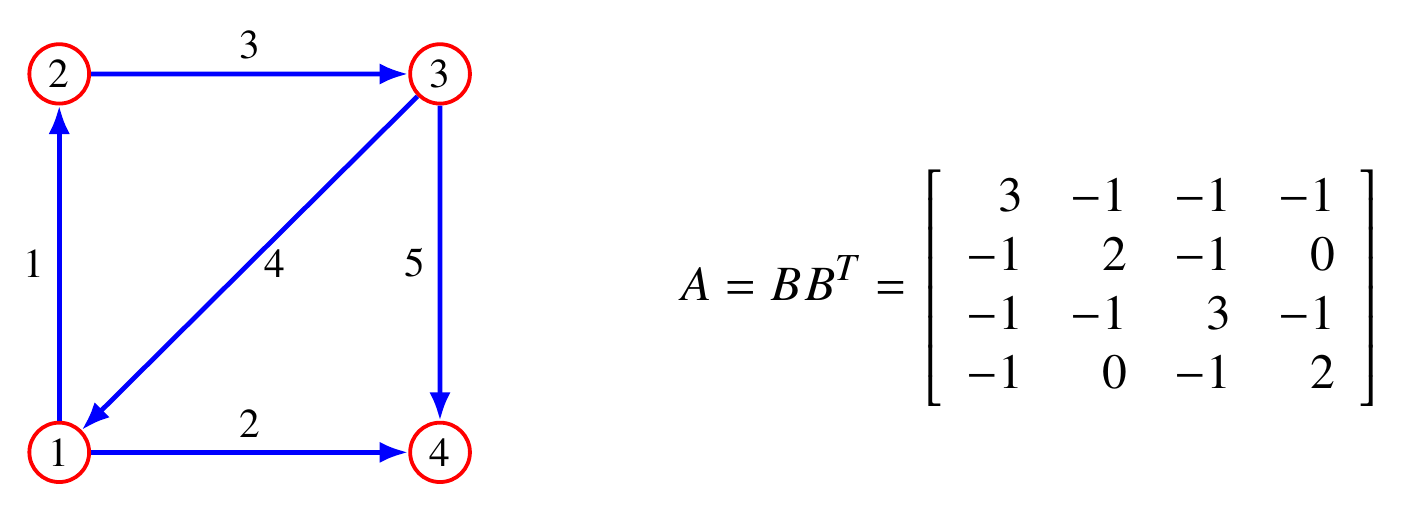
矩阵的逆

对于大部分的应用来说求矩阵的逆都不不必要的。对于求解$Mx=b$，

如果$M$是一般的矩阵采用LU分解的方法将是最快且最好的选择。
如果矩阵$M$是对称且正定（比如Gram矩阵）的话，采用cholesky 分解将是最好的选择。
如果一定要求解矩阵的逆的话，gauss-Jordan消去发可能是最好的选择。

Cholesky factorization

所有的正定矩阵$A\in R^{n\times n}$都可以分解为： $$ A= R^TR $$ 其中$R$是一个上三角矩阵并且它的对角线元素都为正。我们称$R$为$A$的cholesky factor.

cholesky factorization分解算法 1

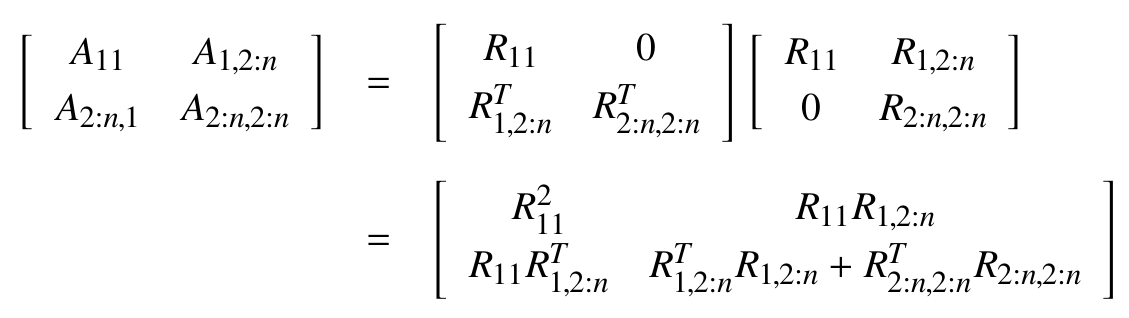
首先计算矩阵$R$的第一行：
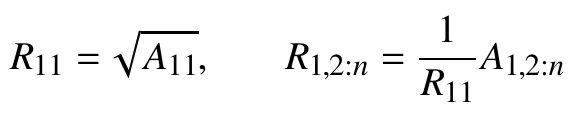
计算矩阵块$R_{2:n,2:n}$ 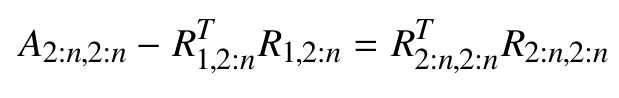可以看出这是$n-1$维的cholesky factorization

cholesky factorization分解算法 2

假定矩阵$B$是一个$m\times n$的矩阵，矩阵$A$是一个Gram矩阵($A=B^TB$)，可以使用QR分解 B=QR. $$ A=B^TB=R^TQ^TQR=R^TR $$

QR分解的方法可以更加的稳定，因为计算过程中不用计算根号。
此方法的时间复杂度维$2mn^2$

应用：

用于求解方程$Ax=b$，其中A是正定的$n\times n$矩阵
1. 分解$A$得到$A=R^TR$
2. 求解$R^TRx=b$
  - 先求$R^Ty=b$
  - 再求$Rx=y$

矩阵逆定理（matrix inversion lemma）

$$ ( A-BD^{-1}C)^{-1} = A^{−1} + A^{−1} B ( D − C A^{-1} B )^{-1} C A^{−1} $$

应用：

$(QQ^T + \sigma_n^2 I_n)^{-1} = \sigma_n^{-2} I_n - \sigma_n^{-2}Q(\sigma_n^2 I_q + Q^TQ)^{-1}Q^T$

矩阵的导数

向量 x 矩阵

假定我们有一个行向量$y \in R^c$由行向量$x \in R^d$ 和矩阵$W \in R^{d \times c}$相乘而来。 $$ y = xW $$

我们来求关于$x$的导数，首先具体来看$y_3$关于$x_7$的导数，已知$y_3 = \sum_{j=1}^d x_j W_{j,3}$,可得$\frac{\partial y_3}{\partial x_7}=W_{7,3}$,所以可以得出导数为

$$ \frac{d y}{d x} = W $$

接下来，我们来求关于$W$的导数，首先具体来看$y_3$关于$W_{7,8}$的导数，已知$y_3 = x_1W_{1,3} + x_2W_{2,3} + \cdots + x_d W_{d,3}$，可得$\frac{\partial y_3}{\partial W_{7,8}}=0$，由此可得$y_3$只有对$W$中第三列求导时才非零其余都为零,即$\frac{\partial y_j}{\partial W_{i,j}}=x_i$。

由于向量y有一个变化的维度，W有两个变化的维度，所以求出的向量应该是一个三维的张量，表示为: $$ F_{i,j,k} = \frac{\partial y_i}{\partial W_{j,k}} $$ 但是只有当$i=k$时，求导结果才非零$F_{i,j,i} = x_j$，所以可以用一个二维的张量进行表示$G_{i,j} = F_{i,j,i}$

矩阵 x 矩阵

假定我们有矩阵 $w \in R^{a, b}, X \in R{b, c}$则$Y \in R{a, c}$: $$ Y = WX $$ 首先我们令$w_i$为矩阵W中的第i行，$y_i$为矩阵Y中的第i行，可知： $$ y_i = w_i X $$ 可得： $$ \frac{\partial y_i}{\partial w_i} = X $$ 且$y_i$关于$w_j(j \neq i)$时导数为全零的矩阵。

接下来，求解$y_i$ 对于$X$的导数：

首先具体分析$y_{i,j} = w_i x_j$可得 $$ \frac{\partial y_{i,j}}{x_j} = w_i^T $$ 其中$w_i^T$为列向量，且$y_{i,j}$对于$x_p (p \neq j)$的导数都为0的列向量。所以可得$y_i$关于$X$的导数可以表示为： $$ \frac{\partial y_{i}}{X} = [w_i^T, \cdots , w_i^T] $$

矩阵的特征值

特征值$\lambda$

设A是一个$n \times n$的矩阵， $\xi$是一个n维非零列向量，若存在一个数$\lambda$,使得 $$ A\xi = \lambda \xi $$ 则称$\lambda$是A的一个特征值，$\xi$为A的属于特征值$\lambda$的一个特征向量。

几何意义

如果把矩阵理解为一个坐标系（不一定直角的，也可能是严重变形的“尺子”），有一类向量叫特征向量，其中的任一个向量，在该坐标系（矩阵）上的投影，都只是自身固定的伸缩。

一个变换矩阵的所有特征向量组成了这个变换矩阵的一组基。所谓基，可以理解为坐标系的轴。我们平常用到的大多是直角坐标系，在线性代数中可以把这个坐标系扭曲、拉伸、旋转，称为基变换。我们可以按需求去设定基，但是基的轴之间必须是线性无关的，也就是保证坐标系的不同轴不要指向同一个方向或可以被别的轴组合而成，否则的话原来的空间就“撑”不起来了。在主成分分析（PCA）中，我们通过在拉伸最大的方向设置基，忽略一些小的量，可以极大的压缩数据而减小失真。

Hermitian matrix

Hermitian matrix: A square matrix such that aij is the complex conjugate of aji for all elements aij of the matrix i.e. a matrix in which corresponding elements with respect to the diagonal are conjugates of each other. The diagonal elements are always real numbers.

$$ \left[ \begin{array}{ccc} 1 & 1 - i & 2 \\ 1 + i & 3 & i \\ 2 & -i & 0 \end{array} \right] $$

Householder Method

Householder's transformation^[8] is aim to find a symmetric tridiagonal matrix T that is similar to a given symmetric matrix A (T and A have same eigenvalues).

Definition: Let $w \in R^n$ with $w^tw = 1$. Then the $n \times n$ matrix $$ P = I - 2ww^t $$ is called a Householder transformation(or Householder matrix).

**Theorem: ** If $P = I - 2ww^t$ is a householder's matrix, then P is symmetric and orthogonal. So $P^{-1} = P^t = P$.

Some basics about the Householder matix;

$Pw = -w$. For any x orthogonal to $w (i.e., \ w^tx = 0)$, then $Px = x$. These imply that P has eigenvalues 1 and -1.
For any two distinct vectors x and y in $R^n$ with same length, the Householder matrix $$ P = I - 2ww^t, $$ $$ w = (x - y)/||x-y||_2 $$ satisfies $$ Px = y. $$

The second property mean given any two vectors x and y, we can find a matrix satisfies $Px = y$. For any $x \in R^n$, let $y = (\pm ||x||_2, 0, \dots, 0)^t \in R_n$, then $||x||_2 = ||y||_2$. There is a Householder matix P such that $Px = y$. This is the key step of Householder method.

Eigensolver Method

The solution to the real or hermitian dense symmetric eigensolver problem usually takes place via three main steps

Reduction of the matrix to tri-diagonal form, typically using Householder Reduction,
Solution of the real symmetric tri-diagonal eigenproblem via one of the following methods:

Bisection for the eigenvalues and inverse iteration for the eigenvectors ^[2],[3]
QR algorithm ^[4],
Divide & Conquer method (D&C) ^[5],
Multiple Relatively Robust Representations (MRRR algorithm) ^[6],

Back transformation to find the eigenvectors for the full problem from the eigenvectors of the tridiagonal problem.

Transform

The set of all eigenvalues is called the spectrum of A and denoted by $spec[A]$.

Transforming A to $A-\tau I$ is called shifting and $\tau \in R$ is called a shift. It is easily verified that $(\lambda, x)$ is an eigenpair of A if and only if $(\lambda - \tau, x)$ is an eigenpair of $A - \tau I$. Thus, the spectrum is shifted by $\tau$ and the eigenvectors are invariant.

Given a nonsingular $Q \in C^{n\time n}$, transforming A to $Q^{-1}AQ$ is called a similarity transformation ot a change of basis. In this case, $(\lambda, x)$ is an eigenpair of A if and only if $(\lambda, Q^{-1}x)$ is an eigenpair of $Q^{-1}AQ$. Thus, the spectrum is invariant under similarity transformations, while the eigenvectors change in a simple way.