liudy

Deep Learning Activation Functions

本文记录深度学习中常用的激活函数
 Study  1011  3 分钟  

Sigmoid

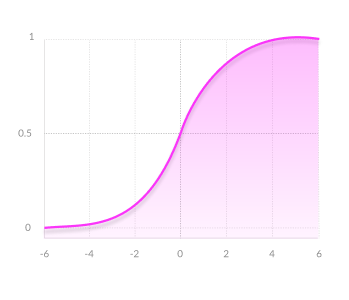
$$ y = sigmoid(x) = \frac{1}{1 + e^{-x}} $$

Derivative: $$ \frac{\partial y}{\partial x} = \frac{1}{1 + e^{-x}} - \frac{1}{(1 + e^{-x})^2} = y(1-y) $$

Advantages

  • Smooth gradient, preventing “jumps” in output values.
  • Output values bound between 0 and 1, normalizing the output of each neuron.
  • Clear predictions—For X above 2 or below -2, tends to bring the Y value (the prediction) to the edge of the curve, very close to 1 or 0. This enables clear predictions.

Disadvantages

  • Vanishing gradient—for very high or very low values of X, there is almost no change to the prediction, causing a vanishing gradient problem. This can result in the network refusing to learn further, or being too slow to reach an accurate prediction.
  • Outputs not zero centered.
  • Computationally expensive

hard_sigmoid

Hard sigmoid activation function.

TanH

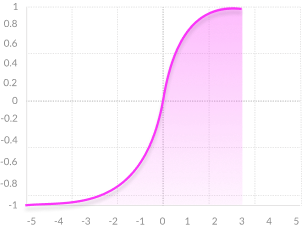
$$ y = tanh(x) = \frac{e^{x} - e^{-x}}{e^x + e^{-x}} = 2 sigmoid(2x) - 1 $$

Derivative: $$ \frac{\partial y}{\partial x} = \frac{4e^{2x}}{(e^{2x} + 1)^2} = (1 + y)(1 - y) $$

Advantages

  • Zero centered—making it easier to model inputs that have strongly negative, neutral, and strongly positive values.
  • Otherwise like the Sigmoid function.

Disadvantages

  • Like the Sigmoid function

ReLU (Rectified Linear Unit)

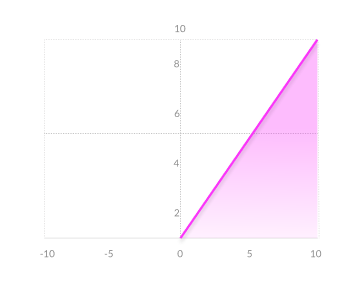
$$ y = max(0, x) $$

Advantages

  • Computationally efficient—allows the network to converge very quickly
  • Non-linear—although it looks like a linear function, ReLU has a derivative function and allows for backpropagation

Disadvantages

  • The Dying ReLU problem—when inputs approach zero, or are negative, the gradient of the function becomes zero, the network cannot perform backpropagation and cannot learn.

Leaky ReLU

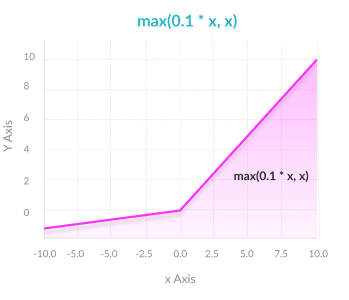
$$ y = \left\{ \begin{array}{rl} x & if \ x > 0 \\ \gamma x & if \ x \leq 0 \end{array} \right. = \max(0, x) + \gamma\min(0, x) $$
where $\gamma$ is a small constant number. When $\gamma < 1$, Leaky ReLU can be written as: $$ y = \max(x, \gamma x) $$

Advantages

  • Prevents dying ReLU problem—this variation of ReLU has a small positive slope in the negative area, so it does enable backpropagation, even for negative input values
  • Otherwise like ReLU

Disadvantages

  • Results not consistent—leaky ReLU does not provide consistent predictions for negative input values.

Parametric ReLU

Parametric ReLU introduces a learnable parameter, different neural could have different parameter. The PReLU for i neural can be written as follow:

$$ y = PReLU_i(x)= \left\{ \begin{array}{rl} x & if \ x > 0 \\ \gamma_i x & if \ x \leq 0 \end{array} \right. = \max(0, x) + \gamma_i \min(0, x) $$
The differences from ReLULayer are:
  1. negative slopes are learnable though backprop
  2. negative slopes can vary across channels. The number of axes of input blob should be greater than or equal to 2. The 1st axis (0-based) is seen as channels.

Advantages

  • Allows the negative slope to be learned—unlike leaky ReLU, this function provides the slope of the negative part of the function as an argument. It is, therefore, possible to perform backpropagation and learn the most appropriate value of α.
  • Otherwise like ReLU

Disadvantages

  • May perform differently for different problems.

ELU (Exponential Linear Unit)

$$ y = ELU(x)= \left\{ \begin{array}{rl} x & if \ x > 0 \\ \gamma (e^x - 1) & if \ x \leq 0 \end{array} \right. = \max(0, x) + \min(0, \gamma(e^x - 1)) $$
where the $\gamma \geq 0$ is a super parameter

Softplus

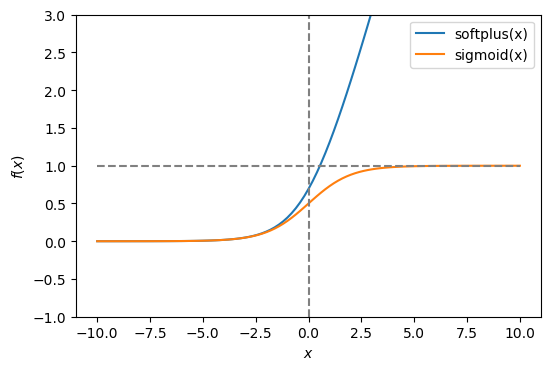The softplus function is a smooth approximation to the ReLU activation function, and is sometimes used in the neural networks in place of ReLU.

$$ y = Softplus(x) = log(1 + e^x) $$ The natural logarithm is the base-e logarithm:

Derivative: $$ \frac{\partial y}{\partial x} = 1 - \frac{1}{1 + e^x} $$

softsign

Softsign activation function

$$ softsign(x) = \frac{x}{abs(x) + 1} = \left\{ \begin{array}{rl} \frac{x}{1 + x} & if \ x > 0 \\ \frac{x}{1 - x} & if \ x \leq 0 \end{array} \right. $$
**Derivative:**
$$ softsign(x) = \left\{ \begin{array}{rl} \frac{1}{(1 + x)^2} & if \ x > 0 \\ \frac{1}{(1-x)^2} & if \ x \leq 0 \end{array} \right. = \frac{y^2}{x^2} $$

In case divide zero, we add 1e-12 to x.

Softmax

Advantages

  • Able to handle multiple classes only one class in other activation functions—normalizes the outputs for each class between 0 and 1, and divides by their sum, giving the probability of the input value being in a specific class.
  • Useful for output neurons—typically Softmax is used only for the output layer, for neural networks that need to classify inputs into multiple categories.

Swish

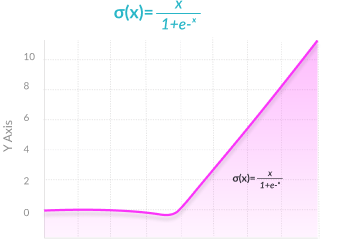$$ y = swish(x) = \frac{x}{1 + e^{-x}} = x * sigmoid(x) $$ Swish is a new, self-gated activation function discovered by researchers at Google. According to their paper, it performs better than ReLU with a similar level of computational efficiency. In experiments on ImageNet with identical models running ReLU and Swish, the new function achieved top -1 classification accuracy 0.6-0.9% higher.

Derivative: $$ \frac{\partial y}{\partial x} = \frac{1}{1 + e^{-x}} + \frac{x}{1+e^{-x}} - \frac{x}{(1+e^{-x})^2} = \frac{y}{x} + y - \frac{y^2}{x} $$

In case divide zero, we add 1e-12 to x.

selu

Scaled Exponential Linear Unit

gelu

applies the gaussian error linear unit(GELU) activation

elu

Exponential linear unit

Reference

  1. 激活函数 sigmoid、tanh、relu
updatedupdated2021-11-062021-11-06

相关文章：