Deep Learning Initializing Weights

Lecun 1998

在输入Standardization以及采用tanh激活函数的情况下，令$n[l-1]Var(w[l])=1$，即在初始化阶段让前向传播过程每层方差保持不变，权重从如下高斯分布采样，其中第𝑙层的fan_in=n[l-1]

Xavier 2010

同时考虑了前向过程和反向过程，使用𝑓𝑎𝑛_𝑖𝑛和𝑓𝑎𝑛_𝑜𝑢𝑡的平均数对方差进行归一化，权重从如下高斯分布中采样

He 2015

文中提到，单独使用上面两个中的哪一个都可以，因为当网络结构确定之后，两者对方差的放缩系数之比为常数。

He初始化方法时和ReLU激活函数

fan_in 与fan_out如何计算

对于全连接层： $$ y_i = x_1w_1 + x_2w_2 + \cdots + x_n w_n = \sum_{j=1}^{n} x_j w_j $$ 则fan_{in} = n

对于卷积层，假定有一个2x2的卷积核操作与一个3x3的特征上

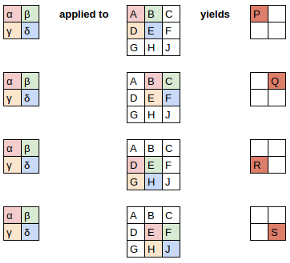
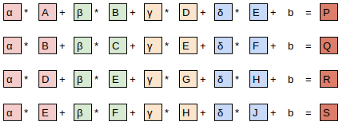
具体的计算表示如下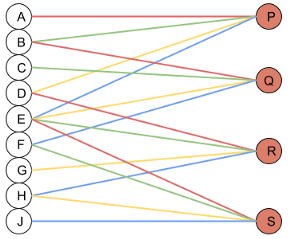： 由图可以看h出每个输出都由4个输入生成，所以fan_in = 4。如果原始的特征有三个通道，则每个输出则有3x4=12个输入生成，则fan_in=12。

1
2
3

receptive_field_size = kernel_height * kernel_width
fan_in = num_input_feature_maps * receptive_field_size
fan_out = num_output_feature_maps * receptive_field_size

即可以理解为:

• fan_in:表示网络参数进行“一次计算”所需的输入单元数目
  • 对于卷积操作表示一次卷积操作所需的输入单元数目
• fan_out:表示网络参数进行“一次计算”会输出的单元数目
  • 对于卷积操作表示对于一块数据进行一次完整卷积操作所需的输出单元数目

pytorch 测试

1
2
3
4
5
6
7

import torch
conv = torch.nn.Conv2d(in_channels=1,out_channels=1,kernel_size=2)
print(f'Conv shape: {conv.weight.shape}')
#returns fan_in and fan_out value for a layer
torch.nn.init._calculate_fan_in_and_fan_out(conv.weight)
print(f'number of elements: {conv.weight.numel()}')
print(f'mean: {conv.weight.mean()} and std: {conv.weight.std()} ')

参考

1. Efficient BackProp
2. Understanding the difficulty of training deep feedforward neural networks
3. Delving Deep into Rectifiers:Surpassing Human-Level Performance on ImageNet Classification
4. Initializing neural networks visualization
5. Don't Trust PyTorch to Initialize Your Variables