全连接层(fully connected layer)
全连接层(fully connected layers,FC)在整个卷积神经网络中起到“分类器”的作用。如果说卷积层、池化层和激活函数层等操作是将原始数据映射到隐层特征空间的话,全连接层则起到将学到的“分布式特征表示”映射到样本标记空间的作用。
全连接的核心操作就是矩阵向量乘积: $Y = XW + b$,本质就是由一个特征空间线性变换到另一个特征空间。其中$Y \in (N, F_o), X \in (N, F_i), W \in (F_i, F_o), b \in (F_o)$.
反响传播(Backward)
假定$Y^{'} \in (N, F_o)$是由后面的层反向传播回来的梯度,可知$\frac{\partial Y_i}{\partial X_i} = W$,其中$Y_i$和$X_i$ 分别代表$Y$和$X$中的一行。所以$\frac{\partial loss}{\partial X_i}$ 可表示为: $$ \frac{\partial loss}{\partial X_i} = \frac{\partial loss}{\partial Y_i} \frac{\partial Y_i}{\partial X_i} = \frac{\partial loss}{\partial Y_i} W^T $$ 其中$\frac{\partial loss}{\partial Y_i} \in (1, F_o)$.
可知$Y_i$对于$W$的导数: $$ G_w = \frac{\partial Y_i}{\partial W} = [X_i^T, \cdots , X_i^T] \in (F_i, F_o) $$ 可得$loss$ 对于$W$的导数: $$ \frac{\partial loss}{\partial W} = \frac{\partial loss}{\partial Y_i} \frac{\partial Y_i}{\partial W} = G_w diag(Y'_i) $$ 其中$diag(Y'_i)$为对角矩阵,其中对角元素为$Y'_i$.
可知$Y_i$对于$b$的导数 $$ \frac{\partial Y_i}{\partial b} = [1, \cdots, 1] \in (1, F_o) $$ 可得$loss$对于$b$的导数为: $$ \frac{\partial loss}{\partial b} = Y'_i \in (1, F_o) $$
ReLU layer
激活函数是用来加入非线性因素的,因为线性模型的表达能力不够。引入ReLU激活函数的优点:
- 采用sigmoid函数,算激活函数时(指数运算),计算量大。而使用Relu,整个计算节省了很多。
- 对于深层网络,sigmoid函数反向传播时,很容易出现梯度消失的情况,(sigmoid接近饱和区的时候,变化太缓慢,导数趋于0)从而无法完成深层网络的训练。
- Relu会使一部分神经元的输出为0,这样就造成了网络的稀疏性,并且减少了参数之间互相依存的关系,缓解了过拟合的发生。
ReLU 函数:
反向传播
loss 对于$X$的梯度为:
Softmax layer
由于实现上使用的时4维的向量,所以softmax层计算时认为的类别数量维$K = CHW$。该层采用的softmax 函数为:
反向传播
对于$Y_{i,j}$,可知其为:
Cross Entropy
cross entropy 是将log_softmax 与 corss entropy 合并而成。表示为: $$ loss(x, class) = -\log(\frac{e^{x[class]}}{\sum_j e^{x[j]}}) = -x[class] + \log(\sum_j e^{x[j]}). $$ 其中x代表一个样本数据,class代表lable标签值。
为了防止出现上溢,在实现上对x进行了额外的操作,$x_i = x_i - x_{max}$。
反向传播
令$f(x_i) = x_i-x_{max}$.
当$i=class$时, loss 对$f(x_i)$求导: $$ \frac{\partial loss}{\partial f(x_{i})} = -f'(x_i) + \frac{e^{f(x_i)}f'(x_i) + \sum_{j \neq i}f'(x_j)e^{f(x_j}}{\sum_j e^{f(x_j)}} $$
当$i \neq class$时, loss 对$f(x_i)$求导: $$ \frac{\partial loss}{\partial f(x_{i})} = \frac{e^{f(x_i)}f'(x_i) + \sum_{j \neq i}f'(x_j)e^{f(x_j)}}{\sum_j e^{f(x_j)}} $$
-
当$i=class$ 且 $x_i = x_{max}$时, loss 对$x_i$求导: $$ \frac{\partial loss}{\partial x_{i}} = \frac{\sum_{j \neq i} -e^{x_j - x_{max}} }{\sum_j e^{x_j - x_{max}}} $$
-
当$i=class$ 且 $x_i \neq x_{max}$时, loss 对$x_i$求导: $$ \frac{\partial loss}{\partial x_{i}} = -1 + \frac{e^{x_i - x_{max}}}{\sum_j e^{x_j - x_{max}}} $$
-
当$i\neq class$ 且 $x_i = x_{max}$时: $$ \frac{\partial loss}{\partial x_{i}} = \frac{\sum_{j\neq i}-e^{x_i - x_{max}}}{\sum_j e^{x_j - x_{max}}} $$
-
当$i\neq class$ 且 $x_i \neq x_{max}$时: $$ \frac{\partial loss}{\partial x_{i}} = \frac{e^{x_i - x_{max}}}{\sum_j e^{x_j- x_{max}}} $$
注意
由于其实对$[x_1, x_2, \cdots, x_n]$进行softmax 与对$[x_1 - x_{max}, x2 - x_{max}, \cdots , x_n - x_{max}]$进行softmax所得结果是一样的, $$ \frac{e^{x_i}}{\sum_j e^{x_j}} = \frac{e^{x_i-x_{max}}}{\sum_j e^{x_j - x_{max}}} $$ 所以我们可以$x_i - x_{max}$视为一种特殊的实现,在求反向传播时可以忽略这个$x_{max}$而直接对原公式进行求导。
当$i=class$时, loss 对 $x_i$求导:
当$i \neq class$ 时, loss 对 $x_i$求导:
$$
\frac{\partial loss}{\partial x_{i}} = \frac{e^{x_i}}{\sum_j e^{x_j}} \
= Y_i
$$
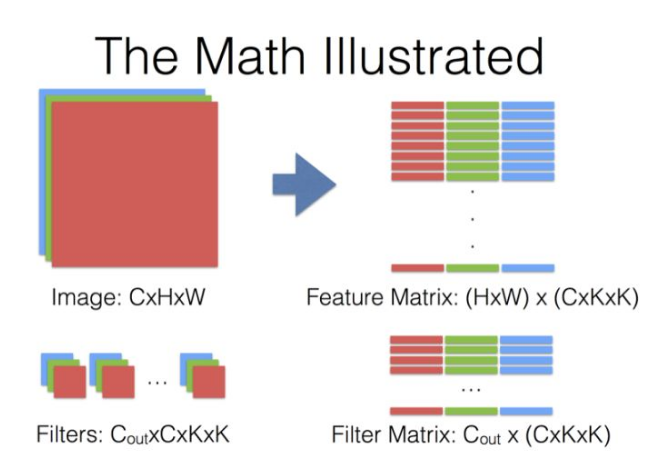
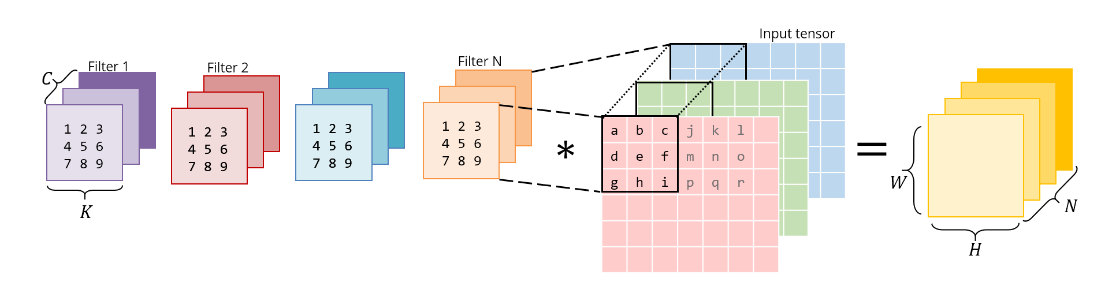
Convolution Layer
Implementation
对于kernel的内存存放顺序为(num_filters, in_channels, k0, k1),对于bias的大小为(num_filters),一个filter对应一个bias参数。
首先对输入特征图像(N, C, H, W)进行一个padding操作得到一个新的特征图像 (N, C, H1, W1), 可得经过卷积操作后所得到的特征图像大小为(N, num_filters, H2, W2)
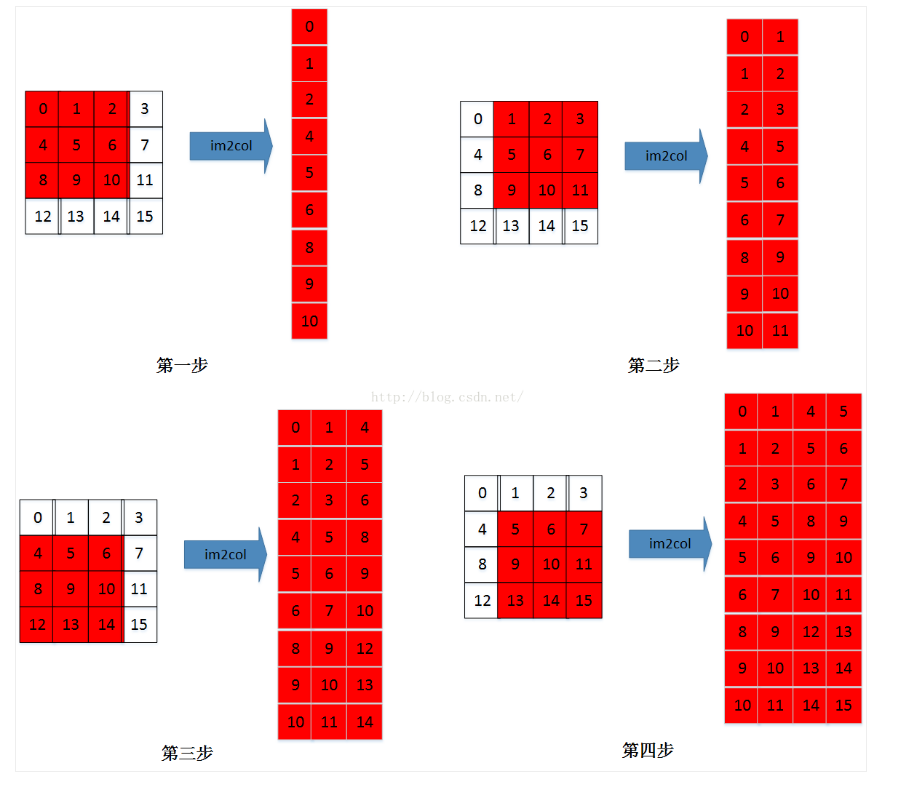
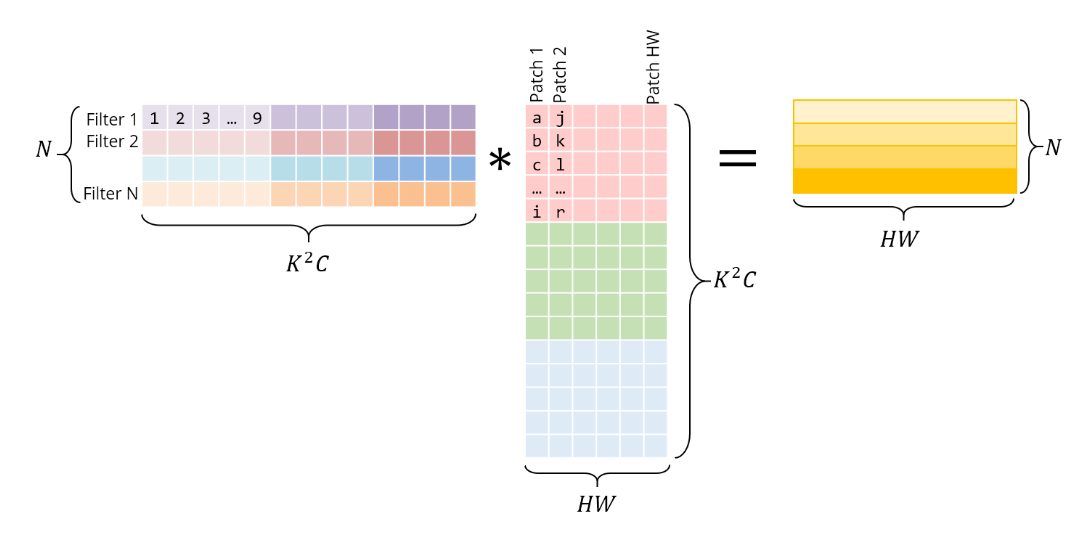
img2col
在img2col操作中每个sample将会转化为一个矩阵大小为(in_channels * k0 * k1, H2 * W2)
假定输入数据如下:
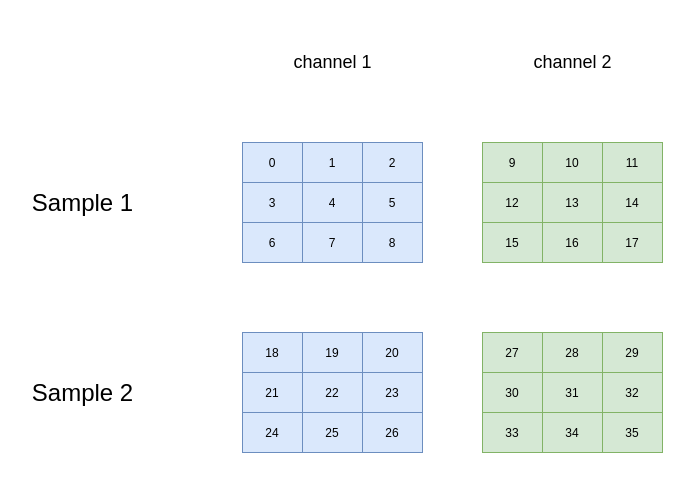
kernel 为(2, 2, 2, 2),strides为(1, 1),则转换后的矩阵为:
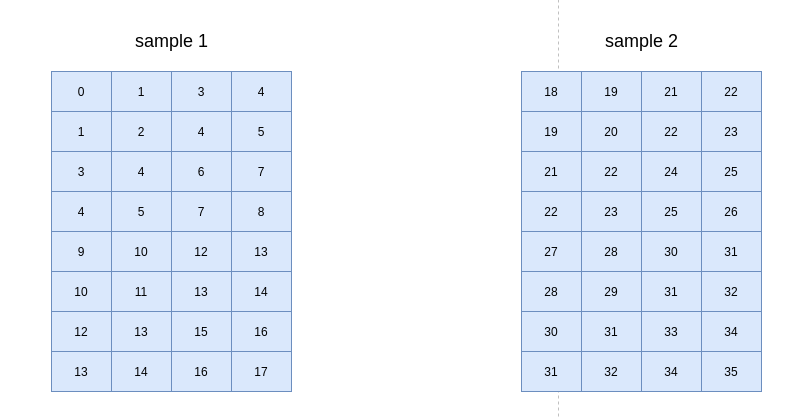
Backward
可知forward的输出结果Output大小为(N, num_filters, H2, H2);
经过转换后forward计算实际是 $$ Y=KM $$ 其中K为卷积核组成的矩阵(num_filters, in_channels * k0 * k1), M为单个样本转换后得到的矩阵(in_channels * k0 * k1, H2 * W2)
Y对K的导数为: $$ \frac{\partial Y_i}{\partial K_i} = (\sum_j M_j)^T $$ 其中$\sum_j M_j$表示将矩阵M按照列的维度进行相加得到一个列向量,$Y_i$代表矩阵Y中的第i行,$K_i$代表矩阵K中的第i行。
引入loss对Y的导数,进而求出loss对K的导数,可得:
Y 对M求导为: $$ \frac{\partial Y_j}{\partial M_j} = (\sum_i K_i)^T $$ 其中$\sum_i K_i$表示将矩阵K按照行的维度进行相加得到一个行向量,$Y_j$代表矩阵Y中的第j列,$M_j$代表矩阵M中的第j列。
引入loss对Y的导数,进而求出loss对M的导数,可得:
Max Pool Layer
对于输入的数据(N, C, H, W),对其中每个通道执行一个基于窗口$(P^h, P^w)$的最大化池的操作。
Implementation
首先对输入特征图像(N, C, H, W)进行一个padding操作得到一个新的特征图像 (N, C, H1, W1), 可得经过池化操作后所得到的特征图像大小为(N, C, H2, W2)
img2col
在img2col操作中每个sample将会转化为一个矩阵
假定输入数据如下:
 经过转换后矩阵表示为:
经过转换后矩阵表示为:
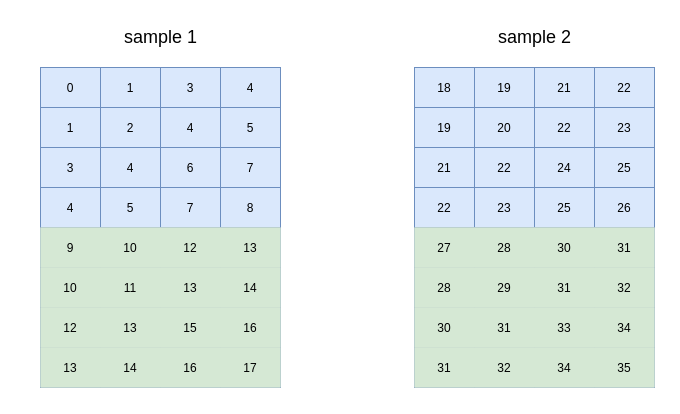 矩阵大小为{$C * H2 * W2, P^h * P^w$}.
矩阵大小为{$C * H2 * W2, P^h * P^w$}.
Drawbacks
- 不能够区分重要的特征是出现一次还是出现了多次,比如,在同一个池化窗口里面最大值出现了多次
- 不能够感知最大值出现的位置信息,位置信息丢失
RNN
对于输入序列中的每个单元,每一层都进行如下计算: $$ h_t = tanh(W_{in}x_t + b_{ih} + W_{hh}h_{(t-1)} + b_{hh}) $$ 其中$h_t, x_t$分别是在t时刻的hidden state和输入。tanh 是非线性激活函数。
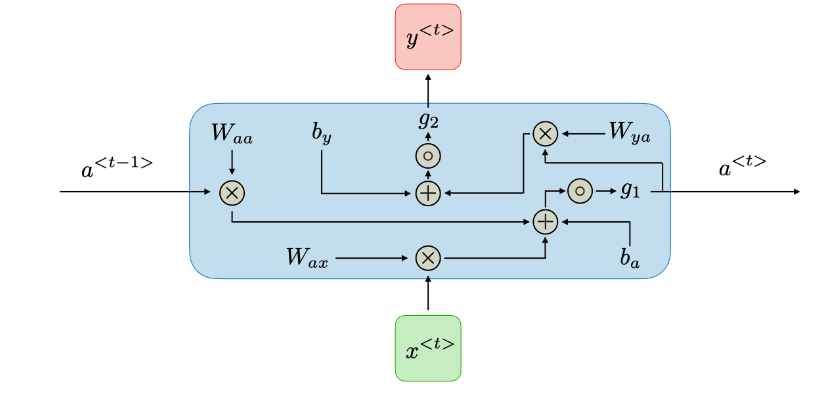
这种典型的RNN的优点:
- 可以处理任意长度的输入序列
- 模型大小没有随着输入大小而增长
- 计算中考虑到了历史信息
- 模型参数在时间的维度上共享
缺点:
- 计算很慢
- 时间跨度长的信息很难获取
- 不能够考虑到未来的信息
Elman RNN
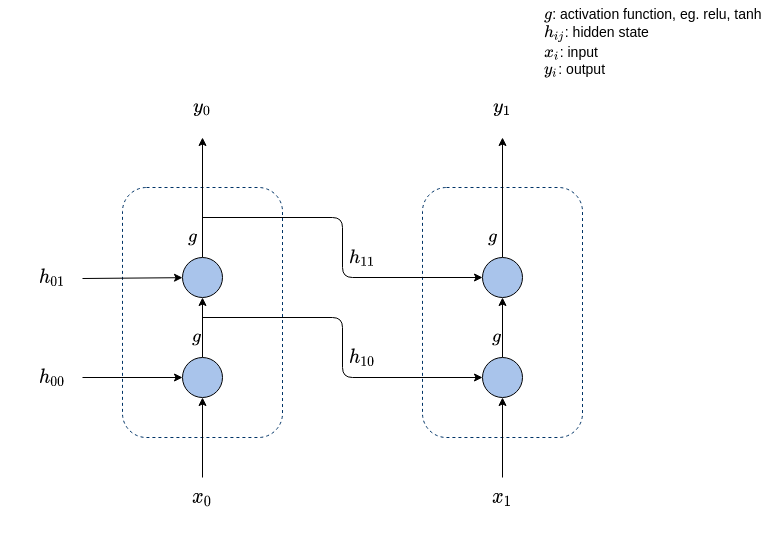 上图展示了pytorch中实现的Elman RNN网络,当num_layers = 2时Elman RNN的网络结构,其中需要注意的是$h_{11} = y_0$.
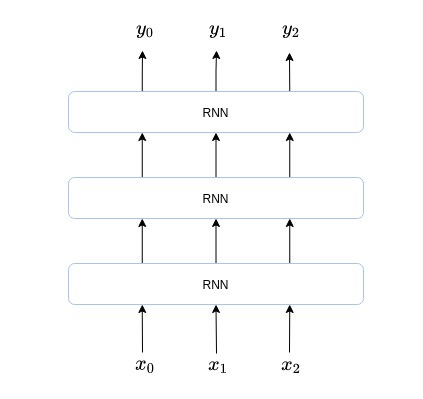
对于不同的num_layer = n可以看成是有n个RNN朝着垂直方向进行堆叠而形成,最上面一个RNN的输出作为模型的输出。
上图展示了pytorch中实现的Elman RNN网络,当num_layers = 2时Elman RNN的网络结构,其中需要注意的是$h_{11} = y_0$.
对于不同的num_layer = n可以看成是有n个RNN朝着垂直方向进行堆叠而形成,最上面一个RNN的输出作为模型的输出。
单层RNN模型可表示为: $$ h_{i + 1} = tanh(x_i W_{ih} + h_i W_{hh} + b) $$
模型中包含的参数:
-
第一层的RNN:$W_{ih} \in R^{input\_size \times hidden\_size}$, $W_{hh} \in R^{hidden\_size \times hidden\_size}$, $b \in R^{hidden\_size}$
-
第二层的RNN:$W_{ih} \in R^{hidden\_size \times hidden\_size}$, $W_{hh} \in R^{hidden\_size \times hidden\_size}$, $b \in R^{hidden\_size}$
Implementation
- 输入数据格式:input(batch, seq_len, input_size), $h_0$(batch, num_layers, hidden_size)
- 输出数据格式:output(batch, seq_len, hidden_size), $h_n$(batch, num_layers, hidden_size)
Backward
对于多层的RNN堆叠,我们可以直接单独分析单个RNN,假定输入的序列长度为2, forward 阶段计算如下:
$y_1$对$x_1$求导: $$ \frac{\partial y_1}{\partial x_1} = \sum_j W_i^j $$
$y_1$对$h_1$求导: $$ \frac{\partial y_1}{\partial h_1} = \sum_j W_h^j $$
$y_1$对$W_i$求导: $$ \frac{\partial y_1}{\partial W_i} = [x_1^T, \cdots, x_1^T] $$
$y_1$对$W_h$求导: $$ \frac{\partial y_1}{\partial W_h} = [h_1^T, \cdots, h_1^T] $$
$y_1$对$b_1$求导: $$ \frac{\partial y_1}{\partial b_1} = \mathbf{1} $$
注意: 在求$y_0$对$x_0, W_i, W_h$求导的时候,要关系到$\frac{\partial y_1}{\partial h_1}$.
LSTM
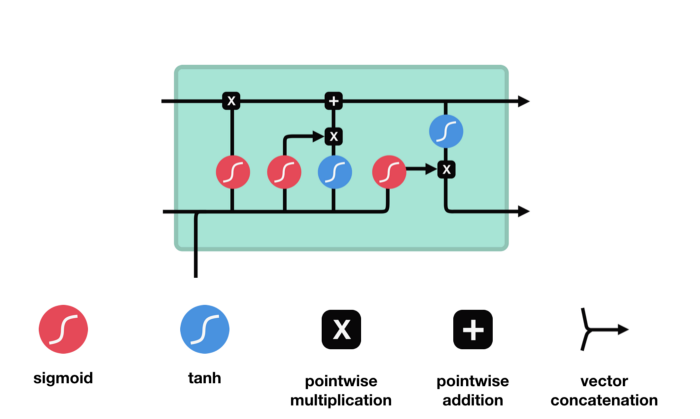
LSTM 中关键的组成为cell state和各种不同的gates。cell state将相关关键信息进行传递。
Implementation
Forward
在计算是我们将($W_{ii}, W_{if}, W_{ig}, W_{io}$)合并为一个矩阵来与输入$x_t$进行相乘:
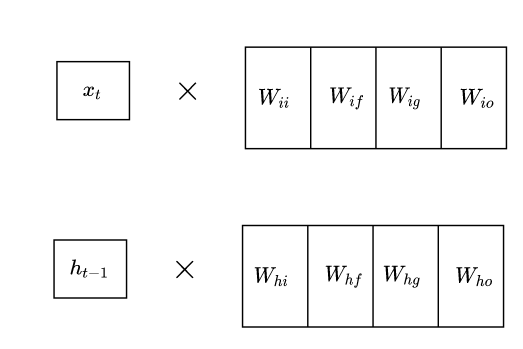 同样的操作用于($W_{hi}, W_{hf}, W_{hg}, W_{ho}$)和$h_{t-1}$
同样的操作用于($W_{hi}, W_{hf}, W_{hg}, W_{ho}$)和$h_{t-1}$
Backward
$h_t$ 对 $o_t$ 求导: $$ \frac{\partial h_t}{\partial o_t} = tanh(c_t) $$ $h_t$ 对 $tanh(c_t)$求导: $$ \frac{\partial h_t}{\partial tanh(c_t)} = o_t $$ $h_t$ 对 $c_t$求导: $$ \frac{\partial h_t}{\partial c_t} = o_t \odot tanh'(c_t) $$ $h_t$ 对 $c_{t-1}$求导: $$ \frac{\partial h_t}{\partial c_t} \frac{\partial c_t}{\partial c_{t-1}}= o_t \odot tanh'(c_t) \odot f_t $$
$h_t$ 对 $f_{t}$求导: $$ \frac{\partial h_t}{\partial c_t} \frac{\partial c_t}{\partial f_{t}}= o_t \odot tanh'(c_t) \odot c_{t-1} $$
$h_t$ 对 $i_{t}$求导: $$ \frac{\partial h_t}{\partial c_t} \frac{\partial c_t}{\partial i_{t}}= o_t \odot tanh'(c_t) \odot g_{t} $$
$h_t$ 对 $g_{t}$求导: $$ \frac{\partial h_t}{\partial c_t} \frac{\partial c_t}{\partial g_{t}}= o_t \odot tanh'(c_t) \odot i_{t} $$ 接下来的求导为忽略sigmoid函数和tanh函数的结果 $c_t$ 对$f_t$求导: $$ \frac{\partial c_t}{\partial f_t} = c_{t-1} $$
$c_t$ 对$i_t$求导: $$ \frac{\partial c_t}{\partial i_t} = g_{t} $$
$c_t$ 对$g_t$求导: $$ \frac{\partial c_t}{\partial i_t} = i_{t} $$
Forget Gate
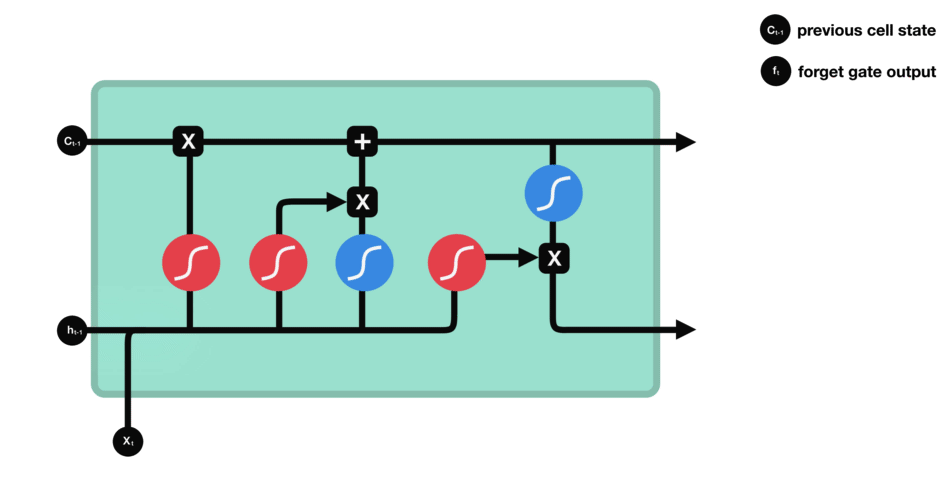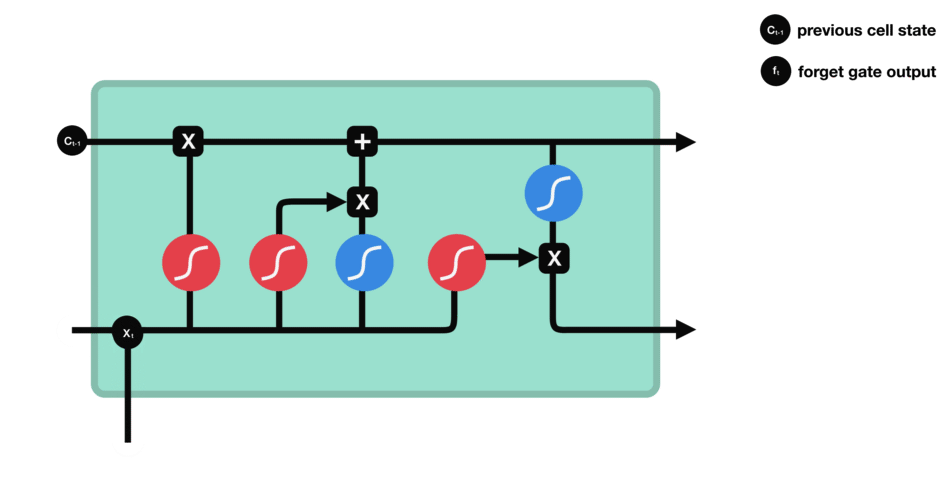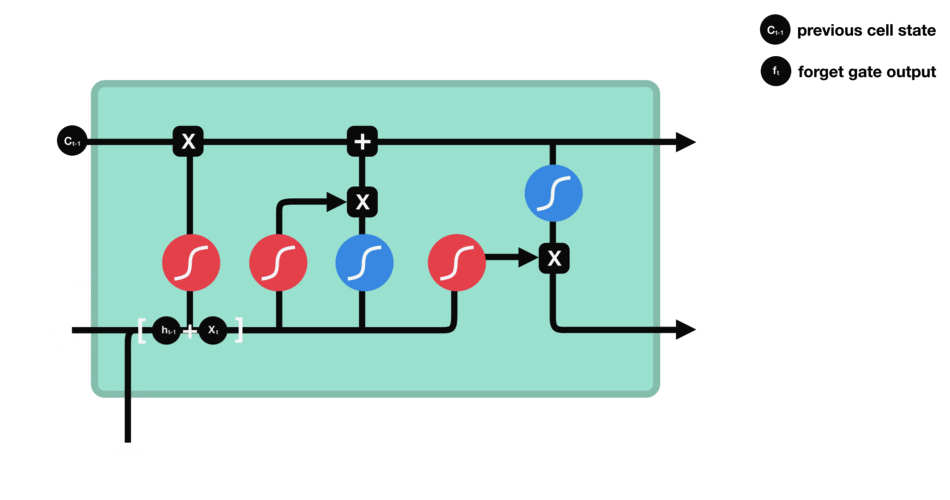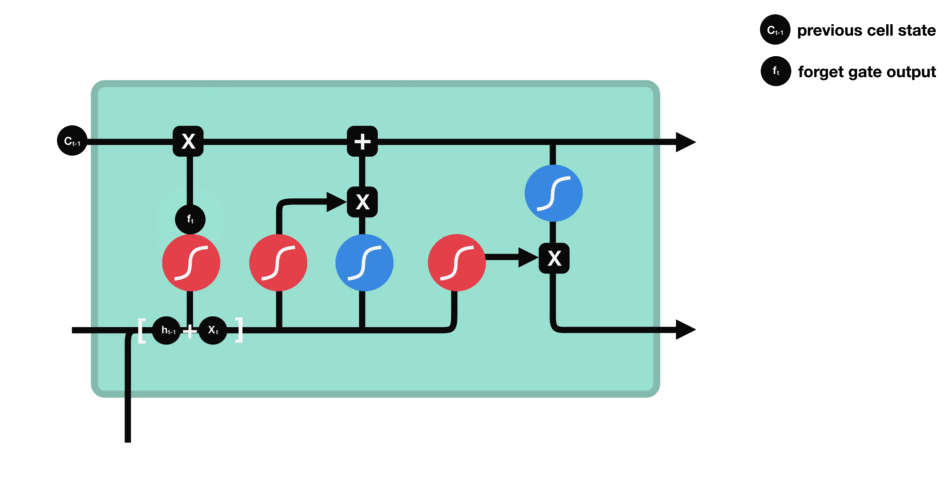
从前面hidden state传来的信息和当前输入传来的信息一起通过sigmoid函数。输出值会在[0,1]之间,越接近0表示需要要忘记,越接近1表示需要保存。
Input Gate
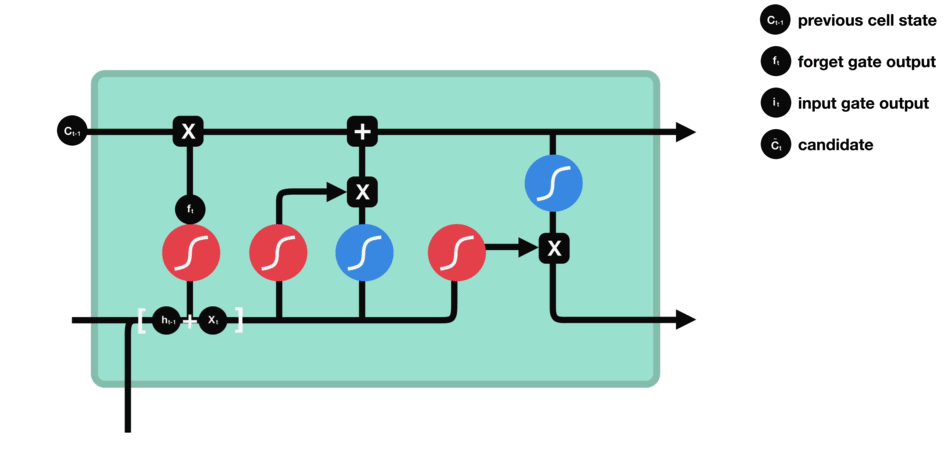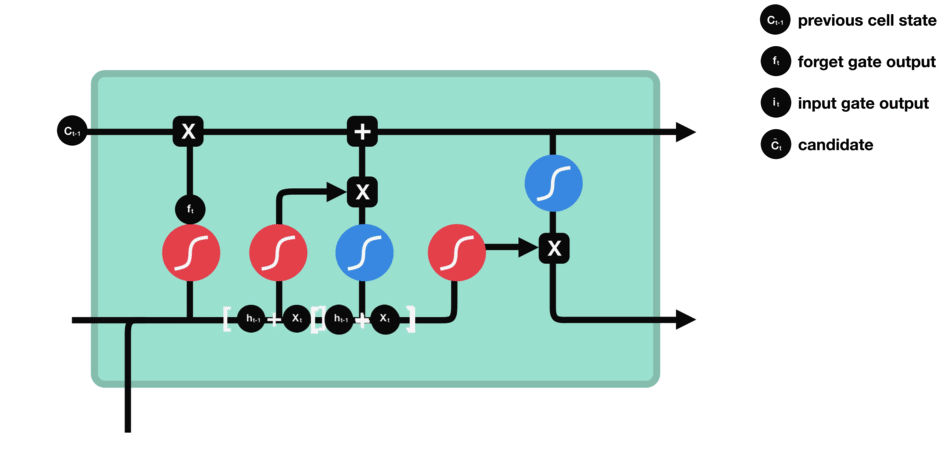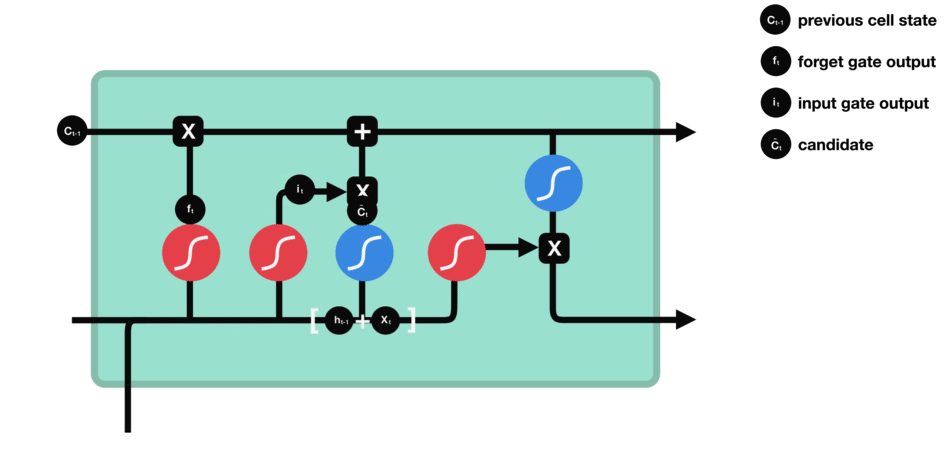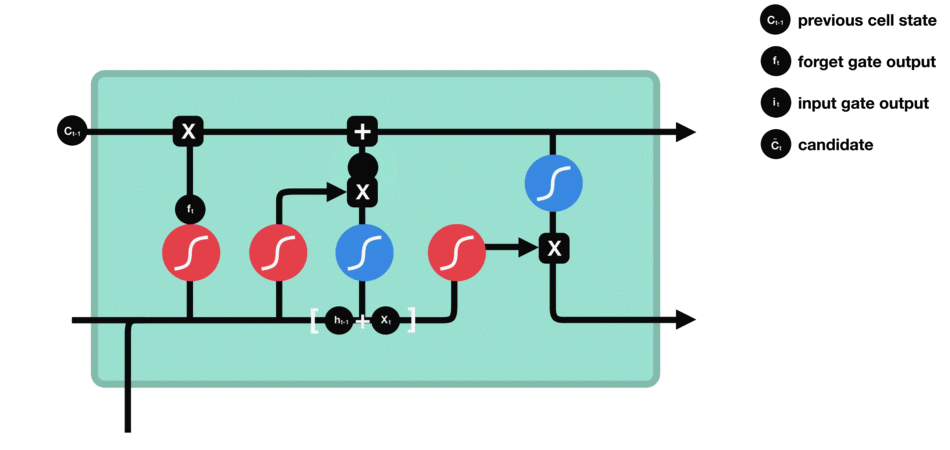
input gate 用于更新cell state。首先将前hidden state 和当前输入x传进一个sigmoid 函数,这个函数会决定哪些值是重要的哪些不重要需要忘记。同时将前hidden state 和当前输入x传进一个tanh 函数将值压缩至[-1, 1]之间帮助归化网络(regulate the network)。之后将sigmodi和tanh处理后的值进行相乘得到最后的结果。
Cell State
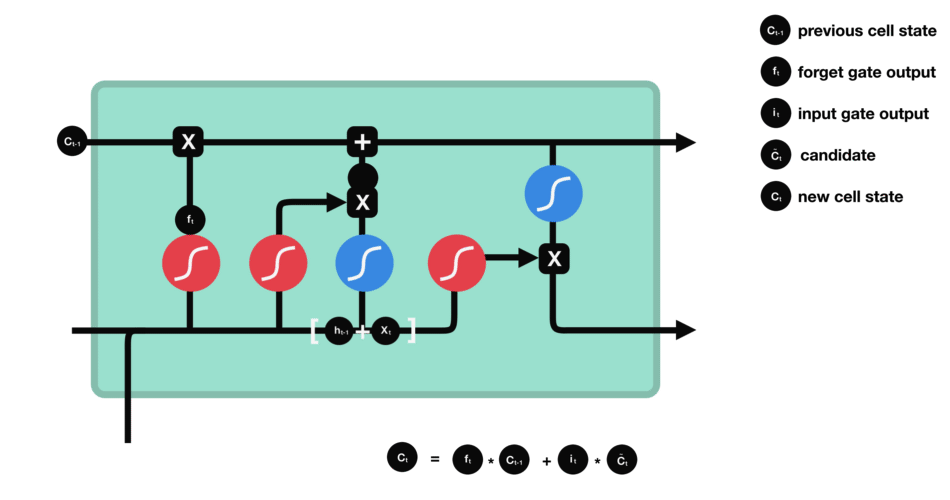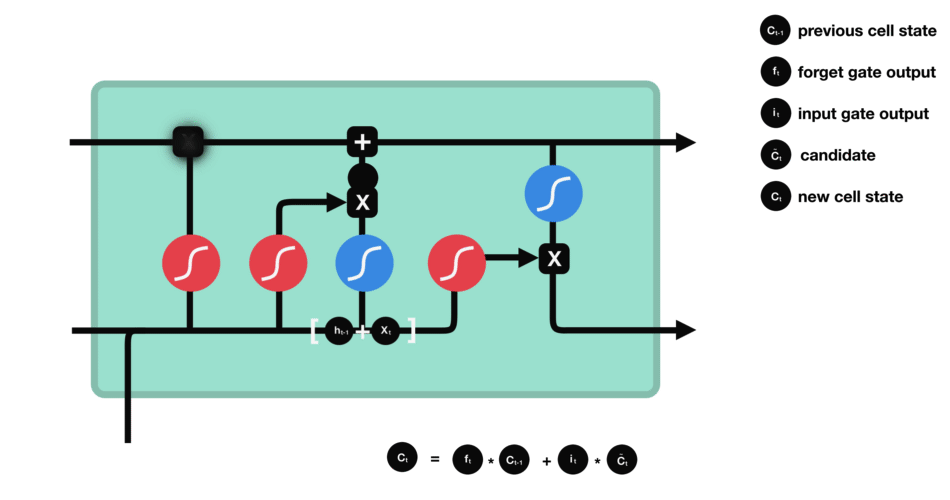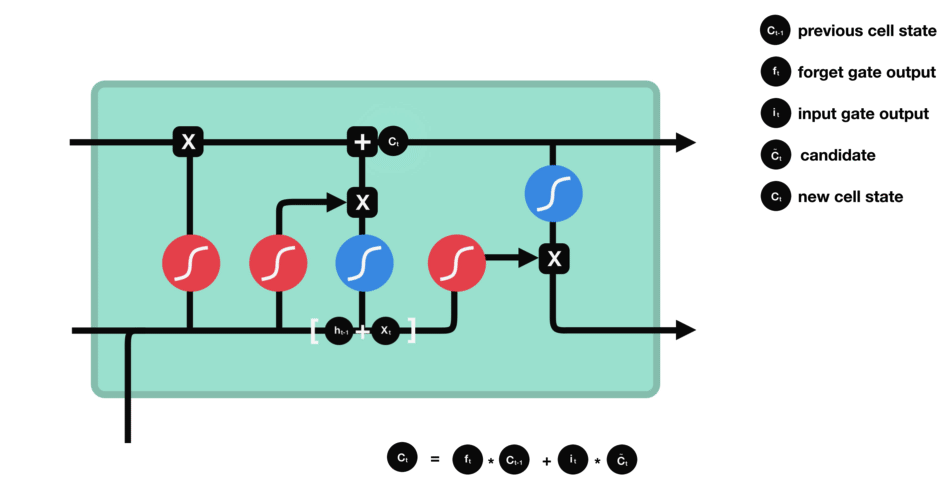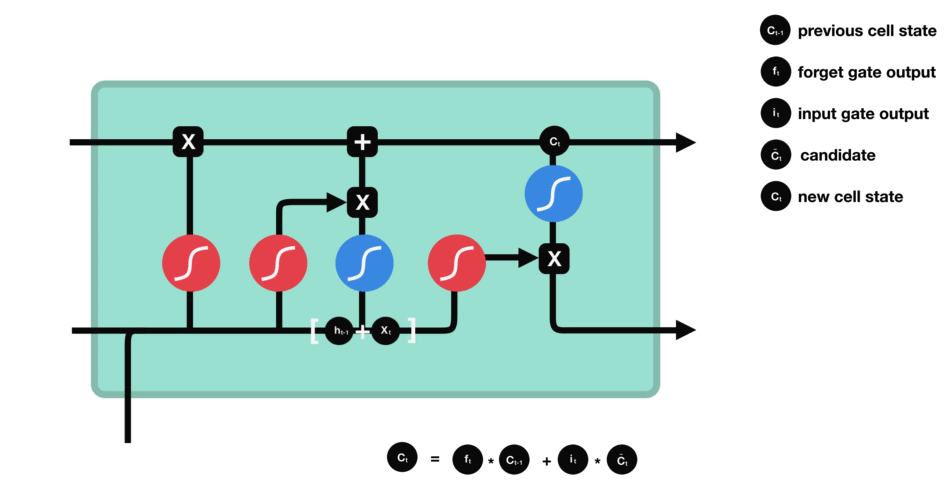
现在我们拥有足够的信息可以计算cell state。首先让cell state与forget gate输出的forget vetor进行相乘。接着与input gate 的结果进行相加生成新的cell state。
Output Gate
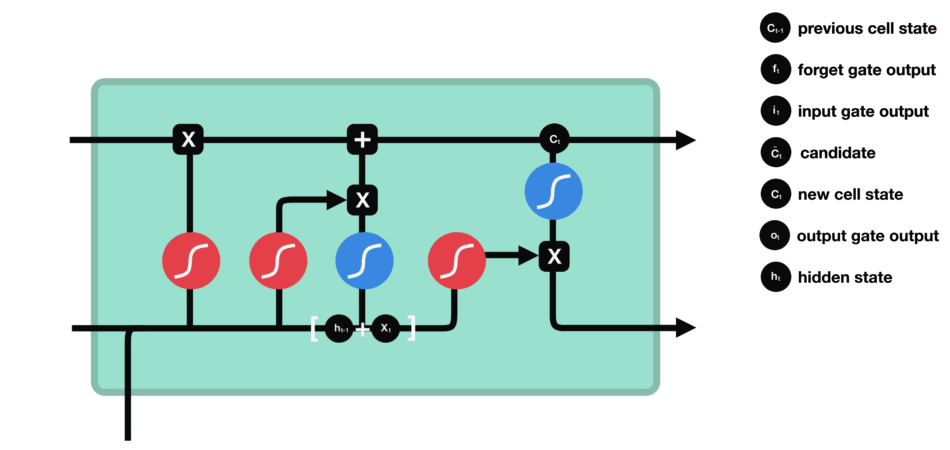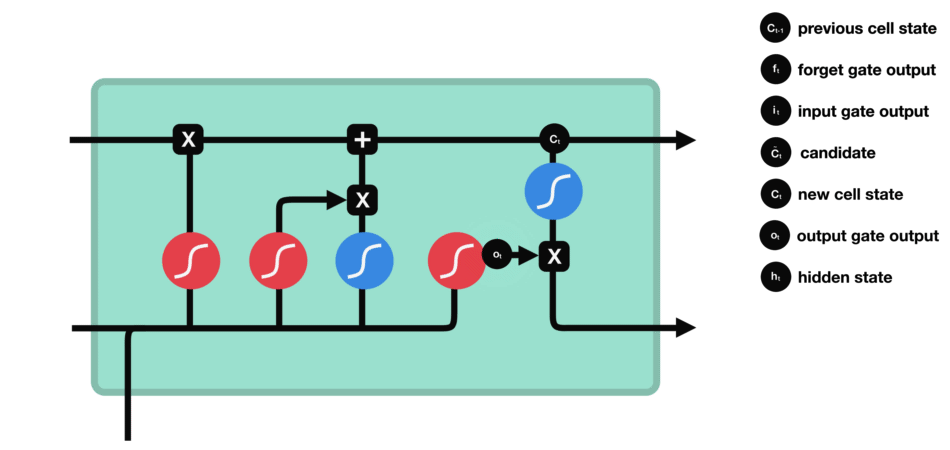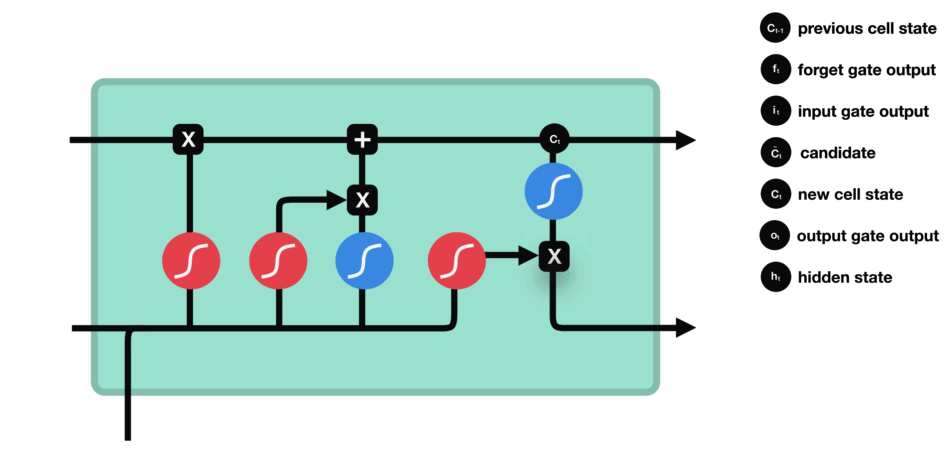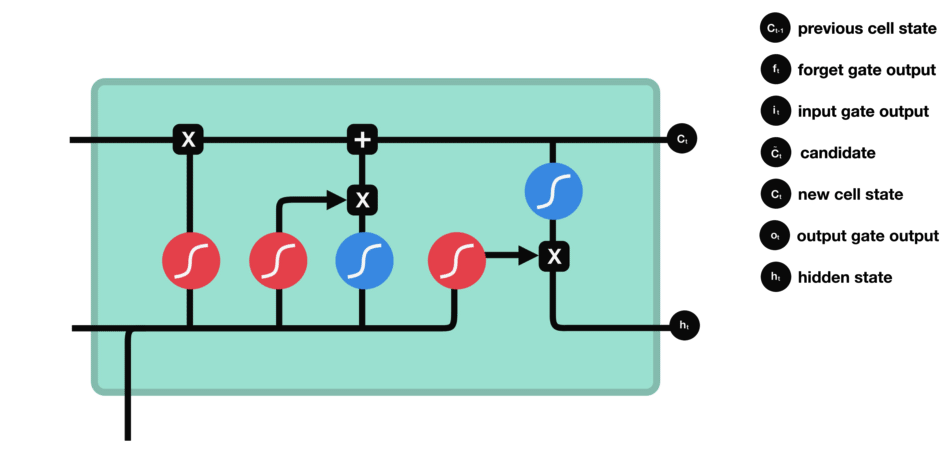
首先,将前hidden state和当前输入x传入sigmoid函数,且将更新后的cell state传入tanh函数,之后将sigmoid和tanh函数的结果进行相乘得到新的hidden state.输出的结果即是hidden state。
GRU
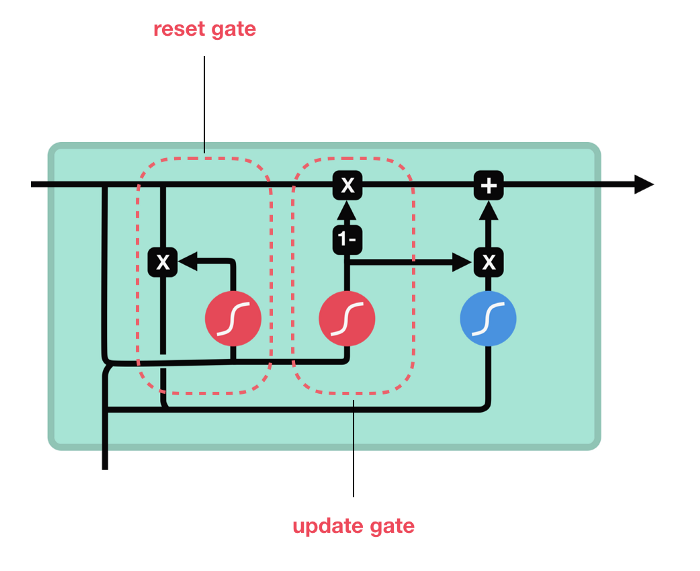 GRU去掉了cell state使用hidden state来传递信息。它只包含两种gates: reset gate 和update gate。
GRU去掉了cell state使用hidden state来传递信息。它只包含两种gates: reset gate 和update gate。
Update gate
update gate 类似于LSTM中的forgate gate和input gate,其决定了丢弃什么信息和添加什么信息。
Reset Gate
reset gate用来决定需要丢弃多少过去的信息。
Dropout
Implementation
在实现上,只需要将输入的X,按照伯努里分布随机的将其中的值赋值为0,然后将处理后的值继续进行前向传播即可。