2-Way Factorization Machines
假定$x \in R^d$表示一个样本的特征向量,y代表标签(可以是实数,或者类的标签值,比如“click/non-click”)。2-way factorization machines 表示为: $$ \hat{y}(x) = \mathbf{w_0} + \sum_{i=1}^d \mathbf{w_i}x_i + \sum_{i=1}^{d} \sum_{j=i+1}^{d} <\mathbf{v_i}, \mathbf{v_j}> x_i x_j $$ 其中$\mathbf{w_0} \in R$ 是一个实数代表global bias,$\mathbf{w} \in R^d$ 是一个向量表示每个特征的重要性,$\mathbf{V} \in R^{d\times k}$ 代表的是feature embeddings,每个特征都用一个$v_i \in R^k$的向量表示,$<\mathbf{v_i}, \mathbf{v_j}>$表示了两个特征之间的交互关系(features interactions)。
对2-way factorizaion mathinces进行复杂度分析可知其计算复杂度为$O(kd^2)$,因为$\sum_{i=1}^{d} \sum_{j=i+1}^{d} <\mathbf{v_i}, \mathbf{v_j}> x_i x_j$ 中$<\mathbf{v_i}, \mathbf{v_j}>$的计算复杂度为k,而后两个$\sum$的复杂度为$d^2$。对于这个高额的计算复杂度而已通过如下公式变换将复杂度降至$O(kd)$:
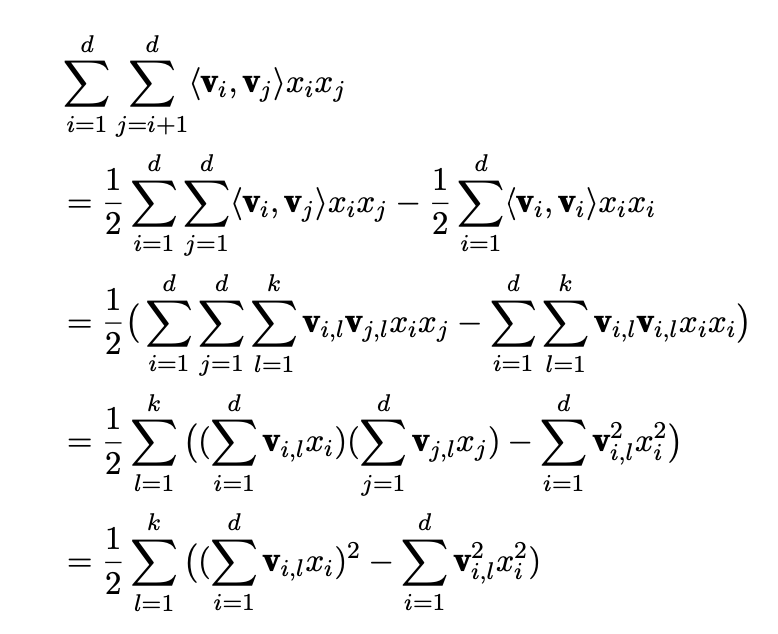
高维的n-way factorization machines 在理论上是可行的,但是在实际中并没有采用因为数值计算不稳定和高额的计算复杂度。
Deep Factorization Mathines
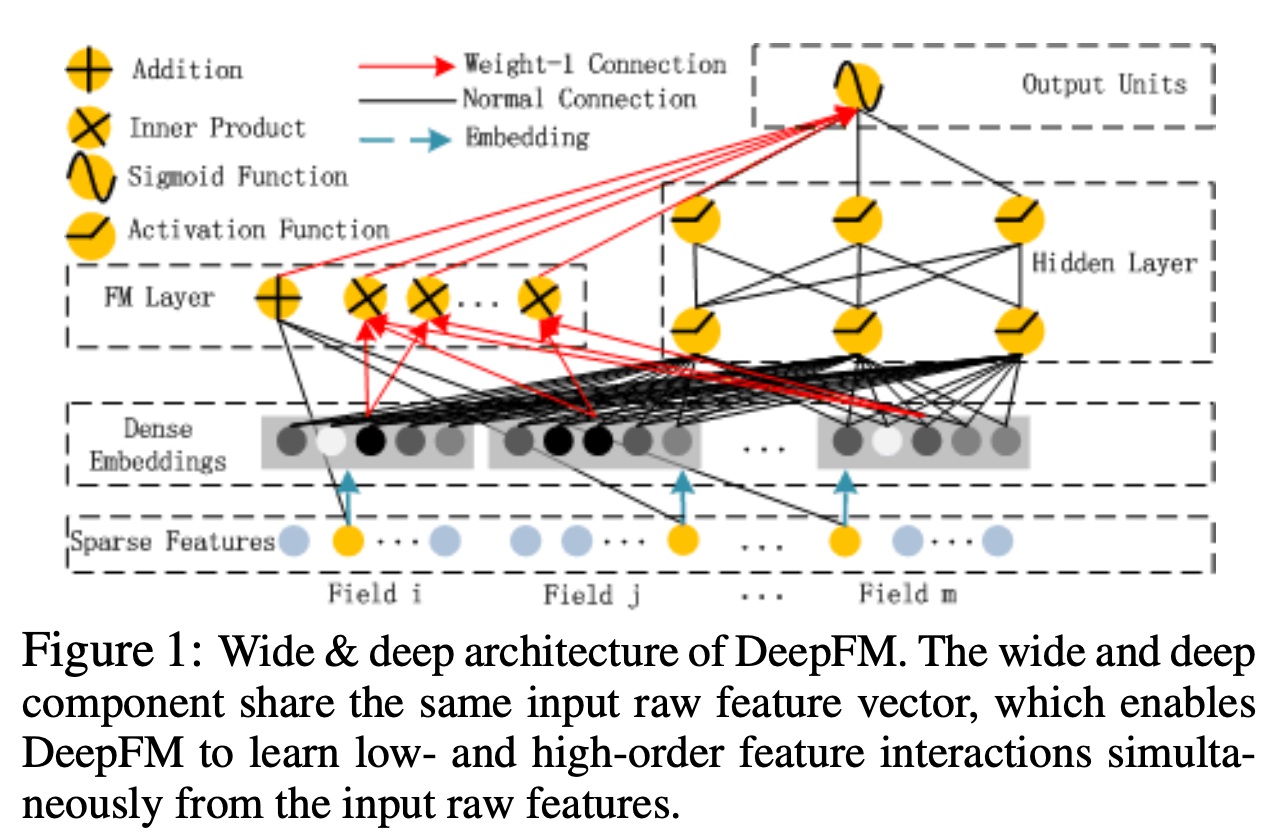 DeepFM consists of two components, FM component and deep component, that share the same input. For feature i, a scalar wi is used to weigh its order-1 importance, a latent vector Vi is used to measure its impact of interactions with other features. Vi is fed in FM component to model order-2 feature interactions, and fed in deep component to model high-order feature interactions.
DeepFM consists of two components, FM component and deep component, that share the same input. For feature i, a scalar wi is used to weigh its order-1 importance, a latent vector Vi is used to measure its impact of interactions with other features. Vi is fed in FM component to model order-2 feature interactions, and fed in deep component to model high-order feature interactions.
Predicted model is as follow: $$ \hat{y} = sigmoid(y_{FM} + y_{DNN}) $$ where $\hat{y} \in (0, 1)$ is the predicted CTR, $y_FM$ is the output of FM component, and $y_DNN$ is the output of deep component.
FM Component
$$ y_{FM} = <w, x> + \sum_{i = 1}^d \sum_{j = i + 1}^d <V_i, V_j> x_i x_j $$ where $w \in R^d$ and $V_i \in R^k$ (k is given).
Deep Component
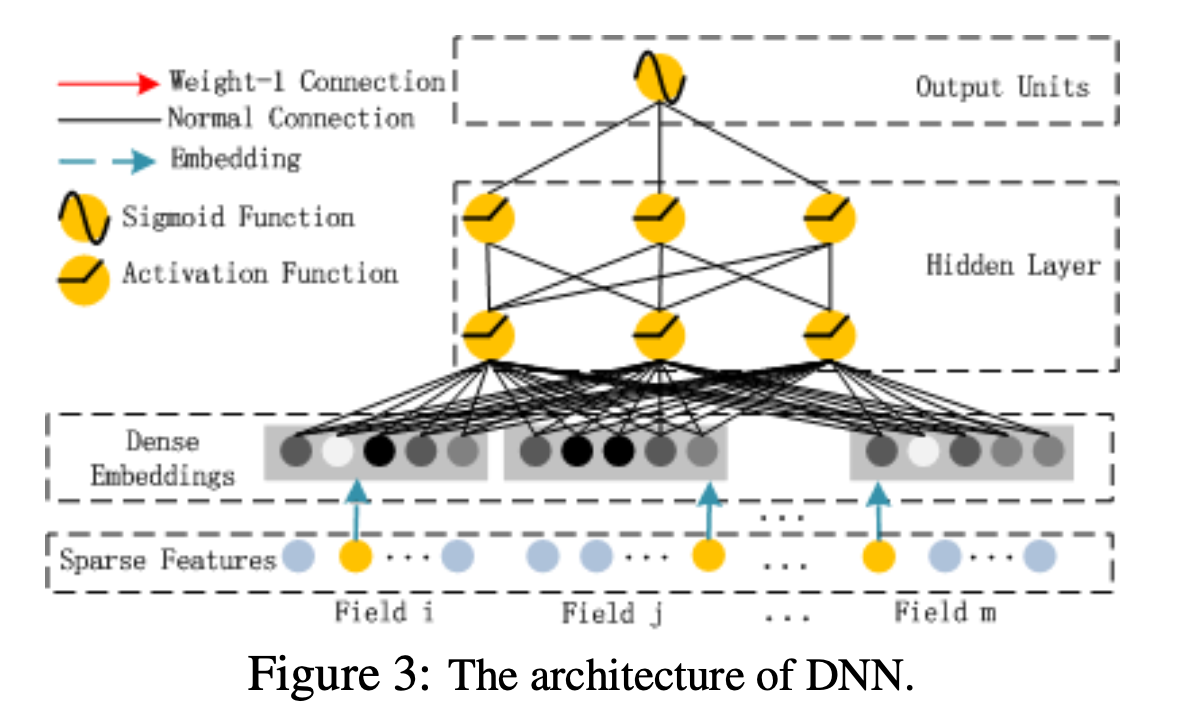 Beacause the raw feature input vector for CTR prediction is usually highly sparse, super high-dimensional, categorical-continuous-mixed, and grouped in fields (e.g., gender, location, age). This suggests an embedding layer to compress the input vector to a low dimensional, dense real-value vector. Embedding layer is as follow:
Beacause the raw feature input vector for CTR prediction is usually highly sparse, super high-dimensional, categorical-continuous-mixed, and grouped in fields (e.g., gender, location, age). This suggests an embedding layer to compress the input vector to a low dimensional, dense real-value vector. Embedding layer is as follow:
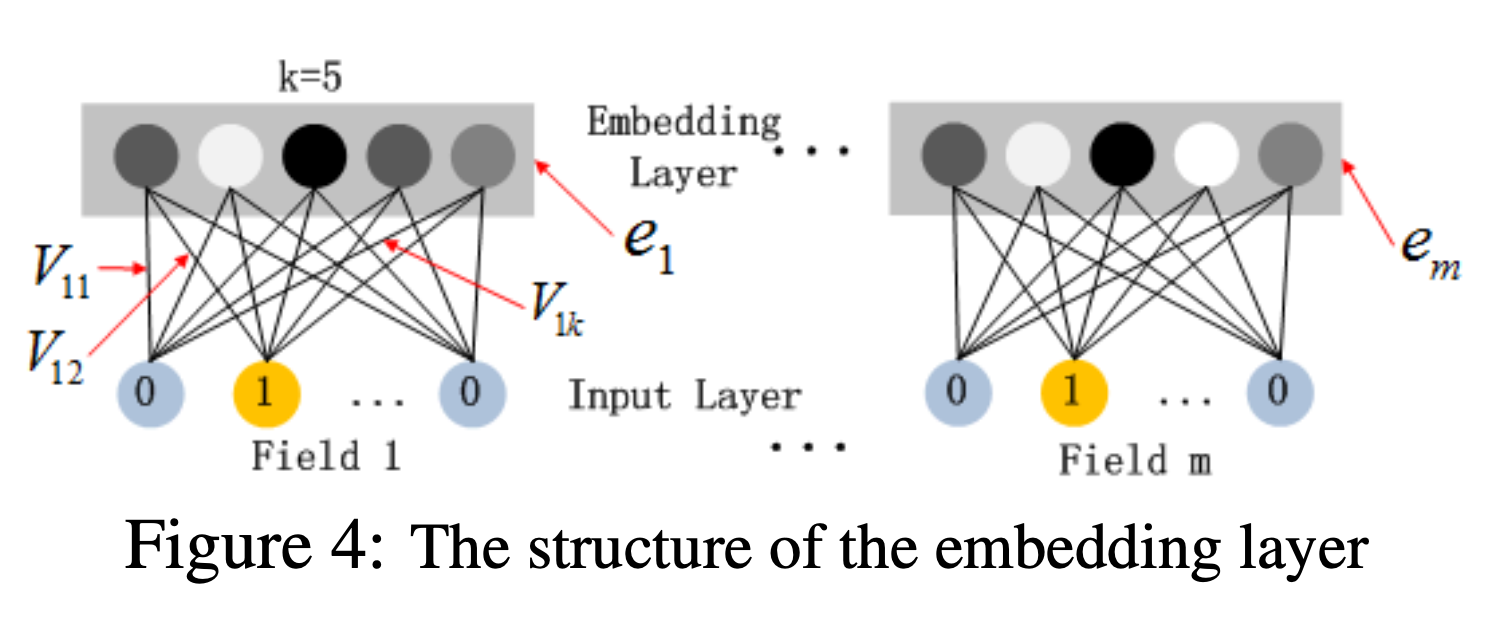 the latent feature vectors (V) in FM now server as network weights which are learned and used to compress the input field vectors to the embedding vectors.
the latent feature vectors (V) in FM now server as network weights which are learned and used to compress the input field vectors to the embedding vectors.
It is worth pointing out that FM component and deep com- ponent share the same feature embedding, which brings two important benefits:
- it learns both low- and high-order fea- ture interactions from raw features;
- there is no need for ex- pertise feature engineering of the input