Momentum
A very popular technique that is used along with SGD is called Momentum. Instead of using only the gradient of the current step to guide the search, momentum also accumulates the gradient of the past steps to determine the direction to go.
$$ v_t = \gamma v_{t-1} + \eta \nabla_{\theta} J(\theta) $$ $$ \theta = \theta - v_t $$
$\gamma$ is momentum term which is usually set to 0.9 or a similar value.
Adagrad
Adagrad is an algorithm for gradient-based optimization that does just this: It adapts the learning rate to the parameters, performing larger updates for infrequent and smaller updates for frequent parameters. For this reason, it is well-suited for dealing with sparse data.
In its update rule, Adagrad modifies the general learning rate $eta$ at each time step t for every parameter $\theta_i$ based on the past gradients that have been computed for $\theta_i$ : $$ \theta_{t+1, i} = \theta_{t, i} - \frac{\eta}{\sqrt{G_{t, ii} + \epsilon}} \nabla_{\theta_t}J(\theta_{t, i}) $$ $$ G_{t, ii} = \sum_{i=0}^{t}\nabla_{\theta_t}J(\theta_{t, i}) \cdot \nabla_{\theta_t}J(\theta_{t, i}) $$ $G_t \in \mathbb{R}^{d \times d}$ here is a diagonal matrix where each diagonal element $i, i$ is the sum of the squares of the gradients w.r.t. $\theta_i$ up to time step t, while $\epsilon$ is a smoothing term that avoids division by zero (usually on the order of $1e−8$).
Since this dynamic rate grows with the inverse of the gradient magnitudes, large gradients have smaller learning rates and small gradients have large learning rates. This is very beneficial for training deep neural networks since the scale of the gradients in each layer is often different by several orders of magnitude, so the optimal learning rate should take that into account. Additionally, this accumulation of gradient in the denominator has the same effects as annealing, reducing the learning rate over time.
However, this method can be sensitive to initial conditions of the parameters and the corresponding gradients. If the initial gradients are large, the learning rates will be low for the remainder of training. This can be combatted by increasing the global learning rate, making the Adagrad method sensitive to the choice of learning rate. Also, due to the continual accumulation of squared gradients in the denominator, the learning rate will continue to decrease throughout training, eventually decreasing to zero and stopping training completely.
Adadelta
Adadelta is an extension of Adagrad that seeks to reduce its aggressive, monotonically decreasing learning rate. Instead of accumulating all past squared gradients, Adadelta restricts the window of accumulated past gradients to some fixed size $w$. Instead of inefficiently storing w previous squared gradients, the sum of gradients is recursively defined as a decaying average of all past squared gradients.
The formula $RMS$ is define as follow:
$$
RMS[g]_t = \sqrt{E[g^2]_t + \epsilon}
$$
And the notation $E[g^2]_t$ is just a variable notation.
RMSprop
RMSprop and Adadelta have both been developed independently around the same time stemming from the need to resolve Adagrad’s radically diminishing learning rates.
Hinton suggests $\gamma$ to be set to 0.9, while a good default value for the learning rate $\eta$ is 0.001.
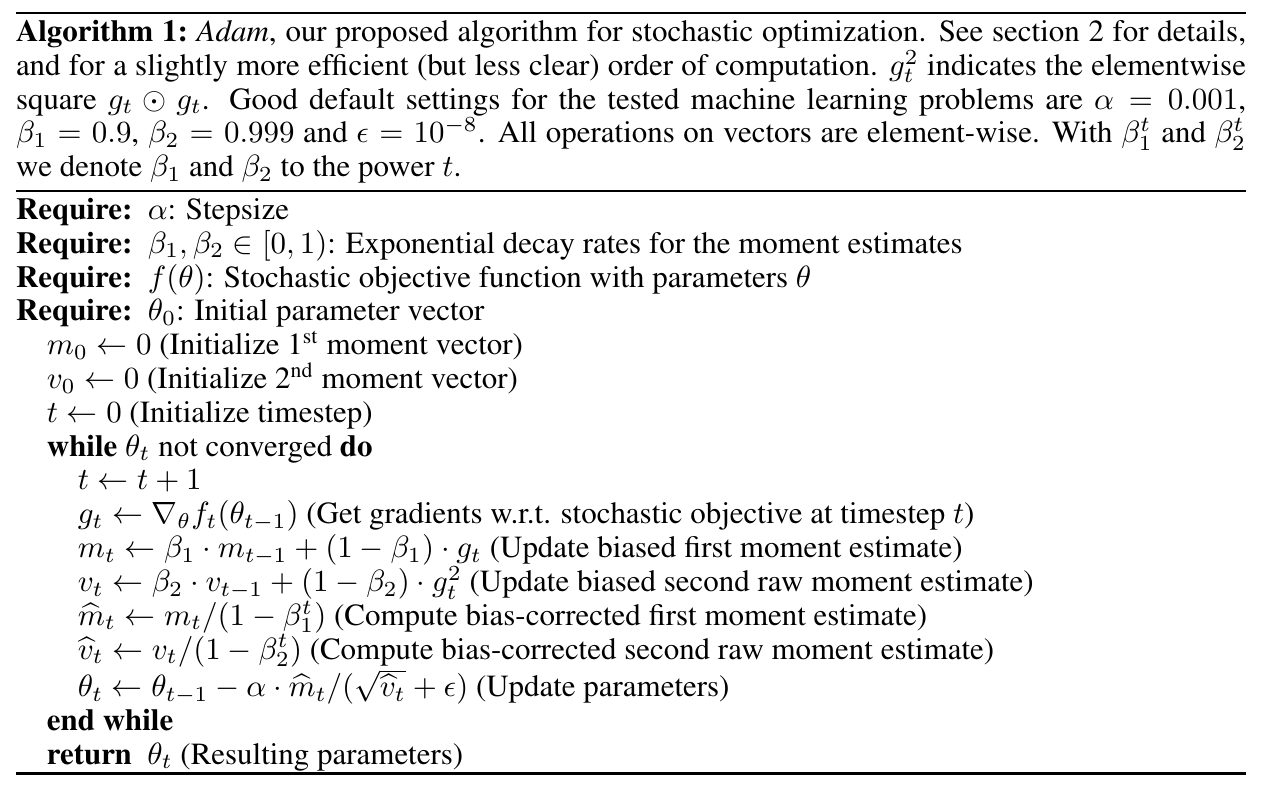
Adam
Adam computes individual adaptive learning rates for different parameters from estimates of first and second moments of the gradients. This method is designed to combine the advantages of AdaGrad and RMSProp.
AdaMax
Notice: in the formulation $\theta_t \leftarrow \theta_{t-1} - (\alpha / (1 - \beta_1^t)) \cdot m_t / u_t$, the $u_t$ can be zero, so we need add a small constant $\epsilon = 1e-12$ to it $\theta_t \leftarrow \theta_{t-1} - (\alpha / (1 - \beta_1^t)) \cdot m_t /(u_t + \epsilon) $