In this papper, we speed up the training process of DNNs applied for automatic speech recognition with CPU+MIC architecture. In this architecture, the training process of DNNs is executed both on MIC and CPU.
parallelism mechanism
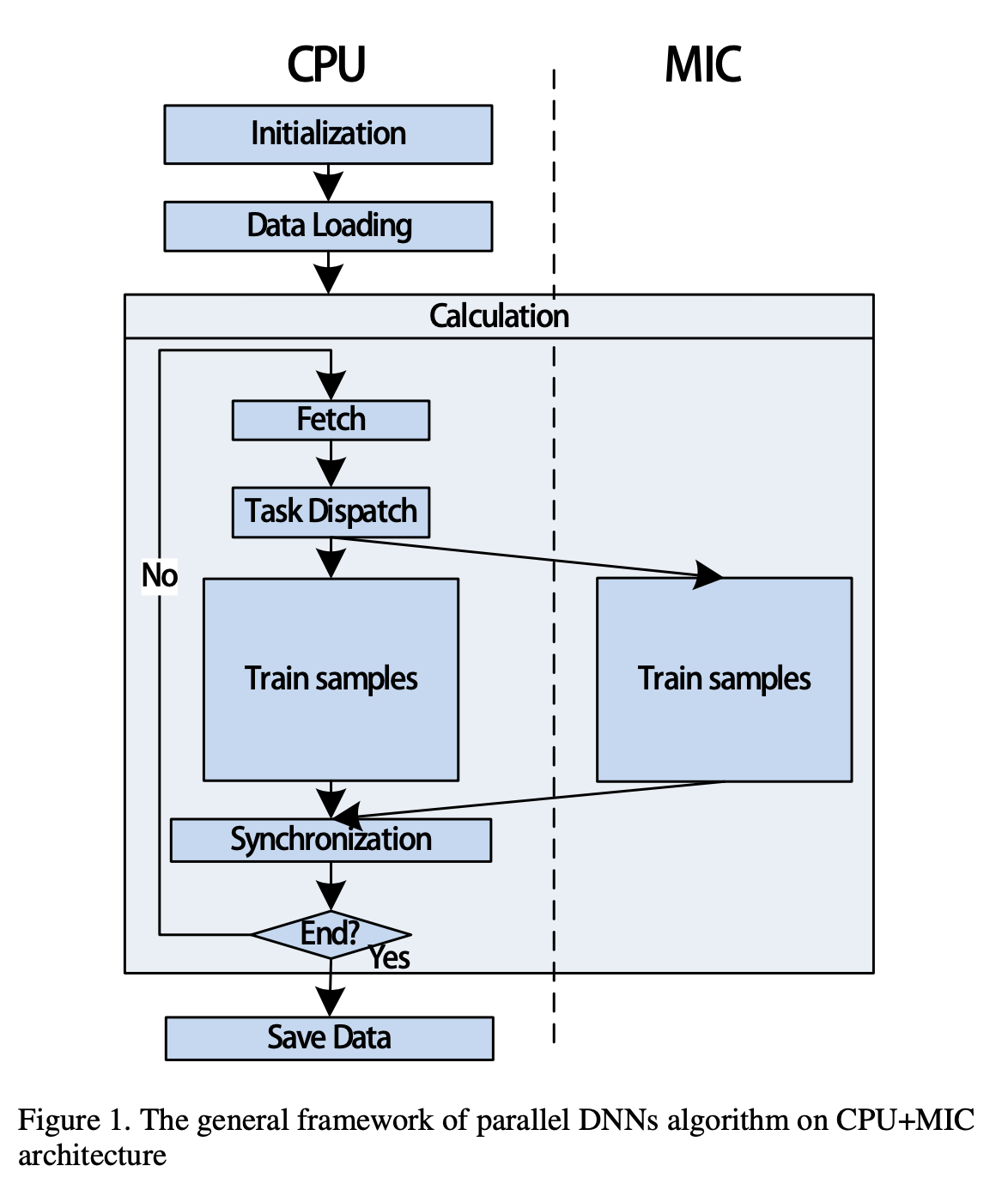 In our research, we divide the batch into two parts which are calculated individually by host (CPU) and MIC. Host and MIC will exchange the parameters of networks sometimes. The synchronization is performed as a result of averaging parameters on Host and MIC. As we all know that the time consumption of data loading from disk to memory cost much. So we apply an asynchronous I/O method to try to hide some latency.
In our research, we divide the batch into two parts which are calculated individually by host (CPU) and MIC. Host and MIC will exchange the parameters of networks sometimes. The synchronization is performed as a result of averaging parameters on Host and MIC. As we all know that the time consumption of data loading from disk to memory cost much. So we apply an asynchronous I/O method to try to hide some latency.
we employ cache- blocking method to improve data locality of program.
IO overlapping
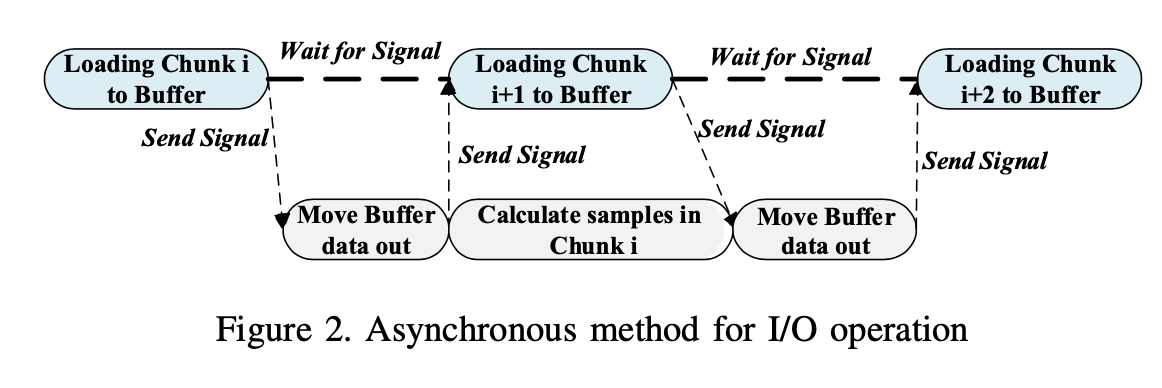 In our method, two threads are created. One is in charge of loading data and the other is responsible for calculating. The control of two threads is based on asynchronous signals supported by pthread library.
In our method, two threads are created. One is in charge of loading data and the other is responsible for calculating. The control of two threads is based on asynchronous signals supported by pthread library.
Parallel Computing in both CPU and MIC
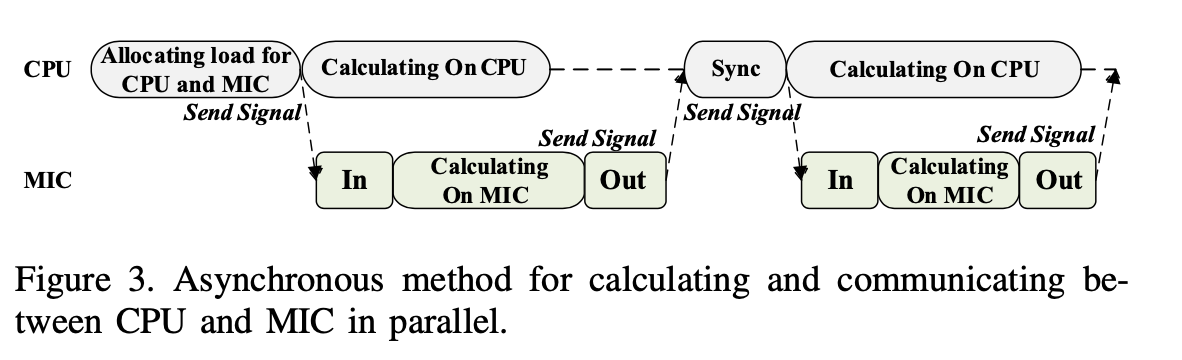 An asynchronous method is also applied in Memory- to-Memory (host to MIC) level. We aim to reduce data transferring cost between CPU and MIC and allow them to calculate independently and simultaneously. The Imple- mentation is slightly different from the method described above. Only one thread is created on the CPU and the signal mechanism is support by MIC’s library.
An asynchronous method is also applied in Memory- to-Memory (host to MIC) level. We aim to reduce data transferring cost between CPU and MIC and allow them to calculate independently and simultaneously. The Imple- mentation is slightly different from the method described above. Only one thread is created on the CPU and the signal mechanism is support by MIC’s library.
Load Balancing Optimization
Load balancing is critical to performance for multi- thread application. The key objective for load balancing is to minimize idle time on threads since an idle core during computation is a wasted resource and will increase the overall execution time of a parallel application.
In our solution, the persen- tage of workload assigned to CPU and MIC is adjusted ac- cording to the historical performance. We regard the number of samples trained per second as the performance measure and record it after training every batch. The load balance between CPU and MIC is achieved by dividing the batch dynamically during iterations.
Actually, the load balance problem can be abstracted as an optimal solution. Let T as the execution time of entire DNNs training, Ti as the execution time of the ith batch and $T_{other}$ as the cost time of other operation like loading data or communication. T can be computed by the formula, $$ T = \sum_{i=1}^N T_i + T_{other} $$ The allocation plan is expressed with P which is a two-tuple (x, 1 − x) and x represents the percentage of workload assigned to CPU, 1 − x represents the percentage of workload assigned to MIC.
To simplify the problem, we assume that change of the allocation plan P has no effect on $T_{other}$. So we can express $T_i$ as follow: $$ T_i = f(x_i) $$ Which is to say, $T_i$ is influenced by the proportion of workload assigned to CPU and MIC, $x_i$. Then we adopt gradient descent method to find optimum allocation P. At first, we need to calculate gradient. We need to use the historical records to calculate gradient approximately in formula, $$ \nabla_{i} = \frac{\partial T_i}{\partial x_i} = \frac{T_i - T_{i-1}}{x_i - x_{i-1}} $$ So we can get the allocation Pi+1 for the i + 1th batch with formula, $$ P_{i+1} = (x_i - \gamma \nabla_i, 1 - x_i + \gamma \nabla_i). $$ In the formula, $\gamma$ is the step length rate which controls the size of load migration when performing load balancing.