Divide and Conquer Kernel Ridge Regression [1]
在这篇论文中主要是使用了"Divide and Conquer"的思想运用于Kernel Ridge Regression算法上,来解决将kernel ridge regression算法在大型数据集上训练导致的高额的计算复杂度($O(N^3)$, $N$为样本的数量)。
首先介绍下"Divide and Conquer"的思想,该思想就是简单的将原本复杂的问题分解成容易解决的小问题,通过解决小问题之后,将小问题的解组合起来得到原复杂问题的解。使用该思想的方法有:归并排序,二分法等。
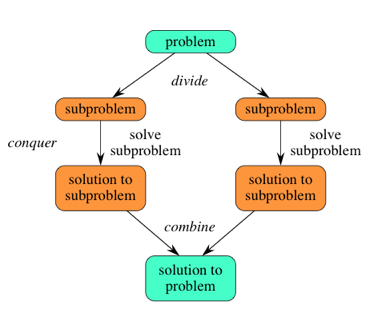
在本文提出对方法是:
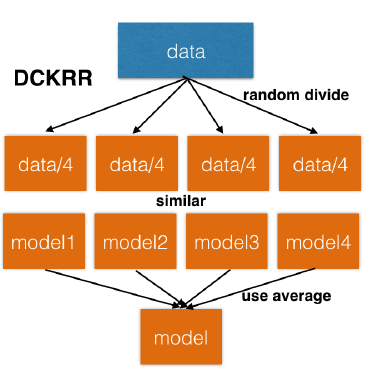
- 首先随机将大小为$N$的数据集分为$m$等份的小数据集
- 基于每个小数据集都独立的训练一个kernel ridge regression模型
$$ \hat{f}_j = \sum_{i=1}^{n} \alpha_i K(x_i,\cdot) \\ \alpha = (K+\lambda I_n)^{-1}y $$其中$\hat{f}_j$代表第$j$个小数据集训练得到的模型,$n$为该小数据集的样本数量大小。
- 最后将所有的模型求个平均得到一个全局的预测模型。 $$ \bar{f} = \frac{1}{m}\sum_{j=1}^m \hat{f}_j $$
注: 在论文《Accurate, Fast and Scalable Kernel Ridge Regression on Parallel and Distributed Systems》中说该方法会产生精度上的损失,没有他的历害。
Accurate, Fast and Scalable Kernel Ridge Regression on Parallel and Distributed Systems[2]
Kernel Ridge Regression 作为一个基本的机器学习的方法。训练该模型所需要的时间复杂度为$O(N^3)$,内存占用为$O(N^2)$(其中$N$为训练样本的大小),如此高额的计算和内存复杂度限制了KRR方法在大数据集上的应用。
在本文提出了两种优秀的方法KKRR2和BKRR2实现了当前最优(本文发表于2018年)
- KKRR2 以精度为目标同时有优秀的速度性能
- BKRR2 以速度为目标同时有优秀的精度
KKRR2
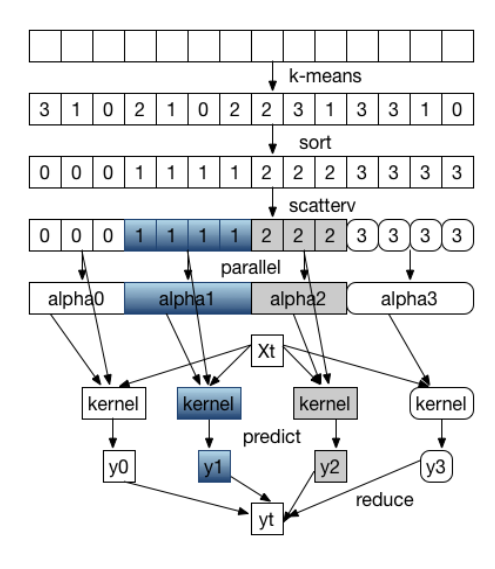
对于两个训练样本,它们的高斯核值(kernel value)计算如下:
$$ \mathcal{k}(x_i, x_j) = \exp^{\frac{-||x_i - x_j||^2}{2\sigma^2}} $$
可以看出当欧几里德距离$||x_i - x_j||^2$越大的时候,该高斯核值越接近0. 所以当给定一个样本$\hat{x}$,只有在欧几里德距离靠近$\hat{x}$的训练样本会对结果有影响。所以我们可以使用K-means方法来对数据集进行划分成组,将欧几里德距离越近的样本点划分为一组 ( 中心点:$CT_1, CT_2, \cdots , CT_k$ ),然后基于各个组,独立的求解一个KRR模型,即可以得到$k$个KRR模型。
对于如何得到最终原问题的解上,由于得到的各个KRR模型都是基于“区别较大”的数据集得来的,所以各个KRR模型之间很不一样。我们不能简单的将各个KRR模型所得到的解进行一个取平均 $\bar{y} = \frac{1}{p} \sum_{i=1}^p y_i$. 而是首先对于输入的样本$\hat{x}$找出距离它最近的中心点$CT_i$,然后将基于数据集$i$所求得的模型$KRR_i$来对样本$\hat{x}$进行预测。
BKRR2
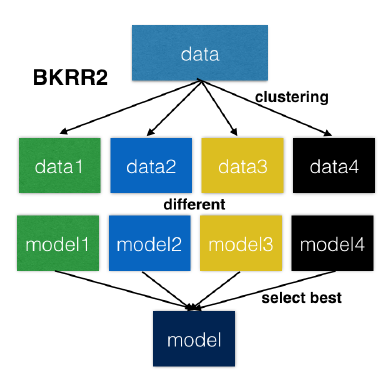
对于以上KKRR2 方法,存在缺点是在使用K-means方法进行数据集分组的时候,各个组所包含的样本数量不均匀,很可能出现有的组包含大量的样本而有点组只有少部分的样本。在多CPU运行时,就会出现负载不均衡的情况,影响执行的速度。
在BKRR2中,作者提出 K-balance clustering 算法实现聚类后各个类别中样本的数量相等。
基本流程是:
- 整个数据集上执行 K-means 算法,得到$k$个中心点{$CT_1, CT_2, \cdots, CT_k$}
- 遍历整个数据集 $n$ 个样本,将其归类到距离它最近的中心点且该聚类的大小没有超过平均大小$\frac{n}{p}$
- 根据更改过平衡后的聚类,重新计算各个类的中心点{$CT_1, CT_2, \cdots, CT_k$}

Implementation
在实现 parallel kernel ridge 回归算法上,我采用的是 BKRR2 方法,但是由于作者提出的 K-balance clustering 需要维持一个对聚类大小的记数,这个在分布式的环境下并不适合。所以我对 balance 进行了不一样的实现。
- 首先训练数据是均分到各个计算节点上,我们采用并行化的 kmeans 算法对这些数据进行聚类,各个节点拥有了对其所有数据的分类标签。
- 进行全局的 cluster size 进行统计,然后进行任务的分配,即各个节点分别负责哪个簇。
- 采用并行化的 balance 策略, 即针对每个 $CT_i$ 我们在各个节点上让它簇大小为 $\frac{sample-size}{N * N}$, 最后合并的时候即可得到大小为 $\frac{sample-size}{N}$ 均匀簇。