Strassen 算法
算法
用于矩阵求逆的Strassen's 算法描述如下：
其中：
$$
\left [
\begin{array}{lr}
A_{11} & A_{12} \\ A_{21} & A_{22}
\end{array}
\right ]^{-1} =
\left [
\begin{array}{lr}
C_{11} & C_{12} \\ C_{21} & C_{22}
\end{array}
\right ]
$$
所以我们可以递归的并行执行，如下：
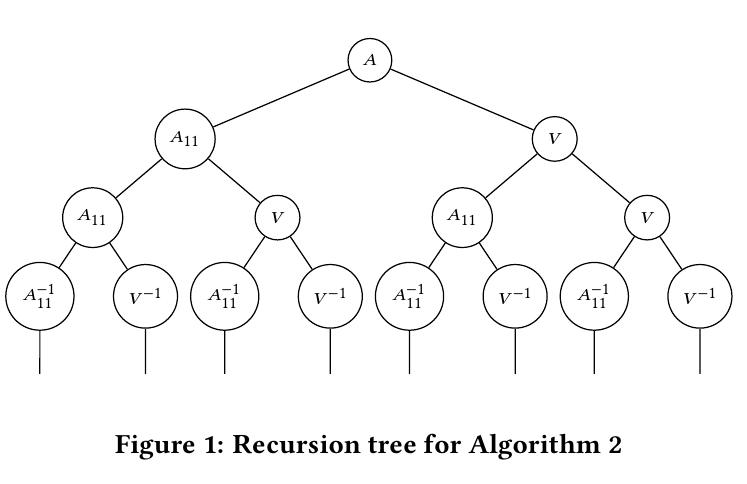
MPI实现上各进程之间的交互关系如下：
Gaussian-Jodan elimination
Gaussian elimination phase
为了增加该方法的稳定性，避免除以0的错误（A[i][i]等于0或者太小）。使用Pivoting操作可以增加稳定性。
-
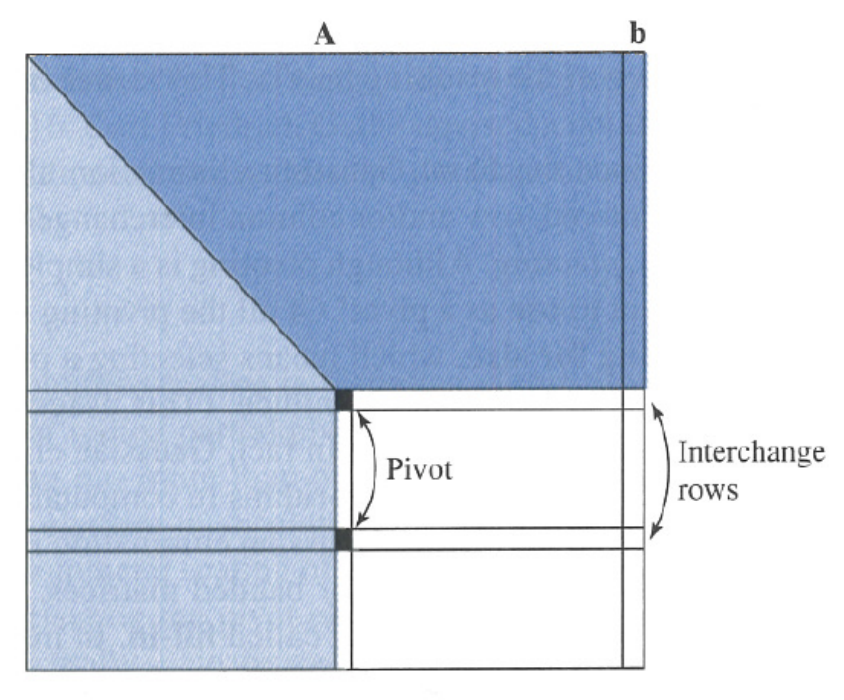
Partial Pivoting: 只交换行
- 往下搜索与pivot位置上拥有最大值的行进行交换
- 通常情况下Partial pivoting即足够了
-
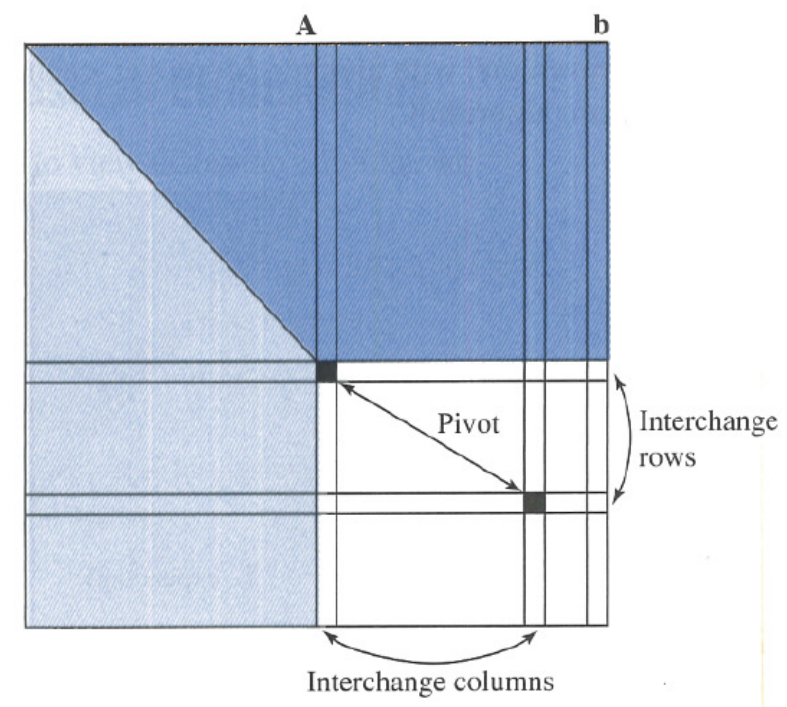
Full Pivoting: 交换行和列
- 从Submatrix中搜索最大的数，然后交换行与列
-
Scaled Partial Pivoting: （有点复杂详情请看4）
Back Substitution Phase
数据分配策略
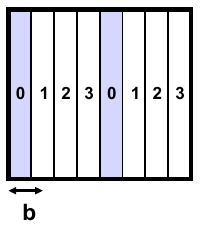
其中d为可控制的变量