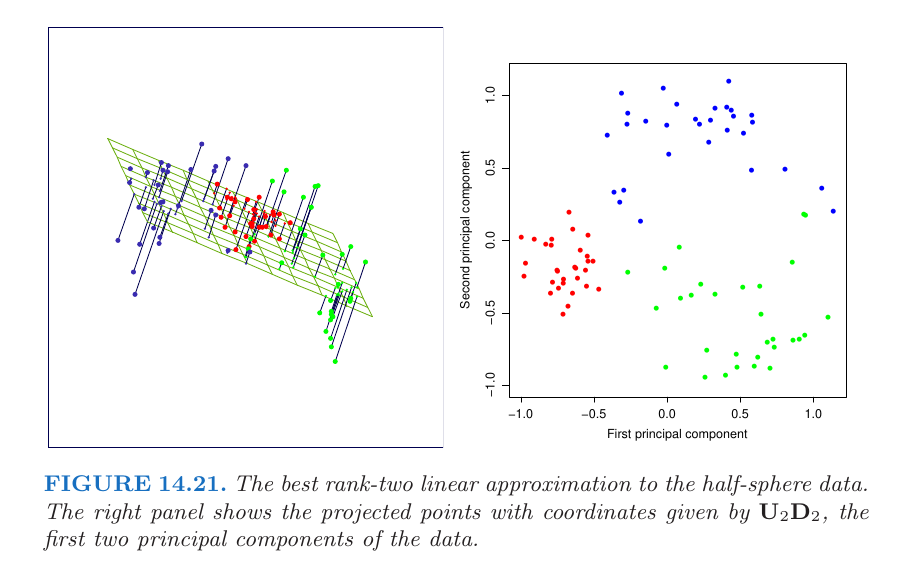
主成分(Principal Components)
假定原数据$x_1, x_2, \cdots ,x_N $的维度是p ($x_i \in \mathbb{R}^p$). 我们使用帙为$q$的线性模型来表示这些数据($q \leq p$): $$ f(\lambda) = \mu + \mathbf{V}_q \lambda $$ 其中$\mu \in \mathbb{R}^p$, $\mathbf{V}_q \in \mathbb{R}^{p\times q}$是由$q$个互相垂直的单位列向量组成,$\lambda \in \mathbb{R}^q$.
确定了模型之后,我们可以使用最小化以下损失函数来减少误差:
$$ \min_{\mu, {\lambda_i}, \mathbf{V}_q}\sum_{i=1}^N(||x_i - \mu - \mathbf{V}_q \lambda_i||)^2 $$
通过对$\mu$和$\lambda_i$求偏导,另其等于0,可以得到: $$ \hat{\mu} = \bar{x} $$ $$ \hat{\lambda_i} = \mathbf{V}^T_q (x_i - \bar{x}) $$ 最后我们就剩下要找到正交矩阵 $\mathbf{V}_q$ 最小化以下函数:
$$ \min_{\mathbf{V}_q} \sum_{i=1}^N (||(x_i - \bar{x} - \mathbf{V}_q \mathbf{V}_q^T (x_i - \bar{x}))||)^2 $$
为了方便我们假定$\bar{x} = 0$ (因为我们可以对原数据进行预处理$\tilde{x} = x_i - \bar{x}$). 我们可以将$\mathbf{H_q = \mathbf{V}_q \mathbf{V}_q^T}$视为投影矩阵(projection matrix)。其将原$x_i$映射到矩阵$V_q$的列空间 (column-space)。
为了找到符合要求的正交矩阵$\mathbf{V}_q$使用的是SVD分解的方法。
$$ \mathbf{X} = \mathbf{UDV}^T $$
其中$\mathbf{U}$是$N\times p$的正交矩阵($\mathbf{U}^T\mathbf{U}=\mathbf{I}_p$)。$\mathbf{V}$是$p\times p$正交矩阵($\mathbf{V}^T\mathbf{V}=\mathbf{I}_p$)。$D$是$p\times p$的对角矩阵 (diagonal matrix)且$d_1 \leq d_2 \leq \cdots \leq d_p \leq 0$. 我们将矩阵$\mathbf{V}$的前$q$个列向量组成的矩阵作为$\mathbf{V}_q$. 而矩阵$\mathbf{UD}$的列向量则称为矩阵$\mathbf{X}$的主成分(principal components)。模型中的最优解$\tilde{\lambda}_i$则是主成分前$q$个列向量($\mathbf{U}_q\mathbf{D_q} \in \mathbb{R}^{N\times q}$),每一行代表一个$\tilde{\lambda}_i$。