Quadratic Discriminant Analysis

LDA and QDA

我们希望对数据进行分类。 Linear DIscriminant Analysis(LDA)和Quadratic discriminant Analysis(QDA)是两种很有名的有监督分类方法 ²。假定我们有数据集{($\mathbf{x}_, y_i$)}, 其中$\mathbf{x}_i \in \mathbb{R}^d$, $y_i \in \mathbb{R}$, $y_i$是类标签。($\mathbf{x}_i$ 是列向量)

在LDA和QDA中首先是基于假设变量是服从高斯分布的，即 $$ f(\mathbf{x}) = \frac{1}{\sqrt{(2\pi )^d |\mathbf{\Sigma}|}}\exp(-\frac{(x - \mathbf{\mu})^T \Sigma^{-1} (x - \mathbf{\mu})}{2} ) $$ 其中$x \in \mathbb{R}^d$, $\mathbf{\mu} \in \mathbb{R}^d$是均值，$\mathbf{\Sigma} \in \mathbb{R}^{d \times d}$是协方差矩阵, $|\cdot|$是矩阵的行列式。

假设现在我们的目标是只有两个类别需要区分$C_1$和$C_2$，它们的先验概率为： $$ P(x\in C_1) = f_1(x) = \gamma_1 $$

$$ P(x\in C_2) = f_2(x) = \gamma_2 $$ 在进行分类时，我们采用下式对样本进行分类:

$$ x \sim \left \{ \begin{array}{lr} \mathcal{N}(\mathbf{\mu}_1, \mathbf{\Sigma}_1), & if \ x \in C_1 \\ \mathcal{N}(\mathbf{\mu}_2, \mathbf{\Sigma}_2), & if \ x \in C_2 \end{array} \right. $$

由于高维的高斯分布的密度函数不好画,请看以下一维的高斯分布图像。

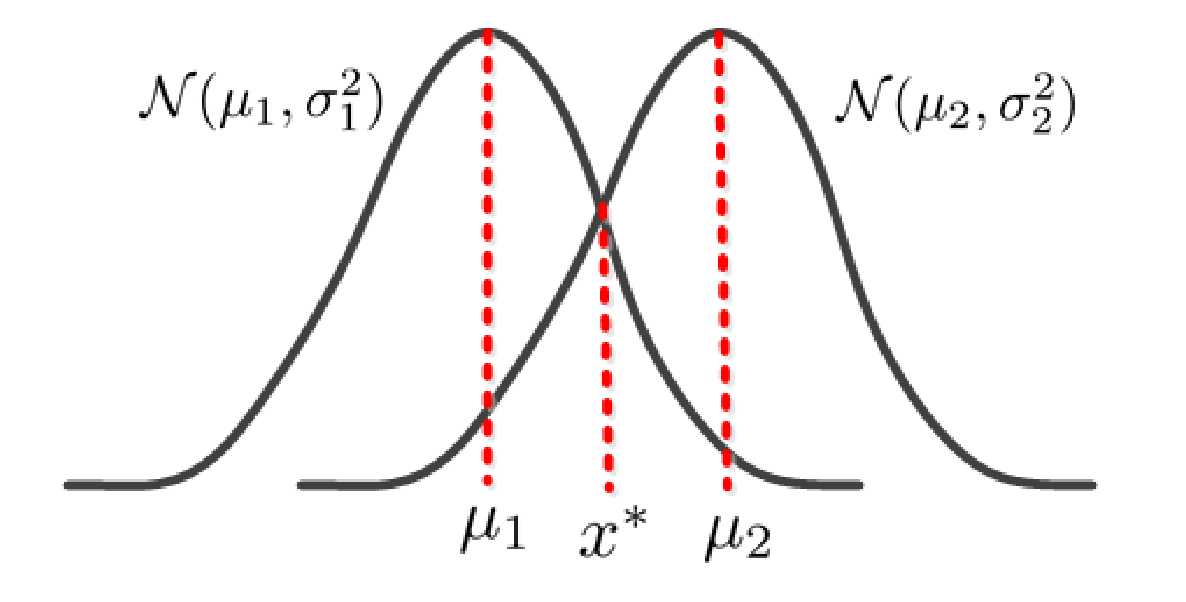
由图可以看出，我们假设两个类别分别服从不同的高斯分布，在分类时会出现分类错误的情况可以表示如下： $$ P(error) = P(x > x^\star , x \in C_1) + P(x < x^\star , x \in C_2) $$ 也可以转化成下式： $$ P(error) = P(x > x^\star | x \in C_1)P(x\in C_1) + P(x < x^\star | x \in C_2)P(x\in C_2) \tag{1} $$ 且由于分布函数的定义我们有： $$ P(x<c, x \in C_1) = F_1(c) $$ $$ P(x<c, x \in C_2) = F_2(c) $$ 所以公式$(1)$我们可以表示为： $$ P(error) = (1-F_1(x^\star ))\gamma_1 + F_2(x^\star)\gamma_2 $$ 我们想要最小化$P(error)$，所以对上式基于$x^\star$进行求导并赋值为0： $$ \frac{\partial P(error)}{\partial x^\star} = -f_1(x^\star)\gamma_1 + f_2(x^\star)\gamma_2 = 0 $$ 求解可得： $$ f_1 (x^\star)\gamma_1 = f_2(x^\star) \gamma_2. \tag{2} $$

在高维的情况下，我们将公式$(2)$具体的表示出来：

$$ \frac{1}{\sqrt{(2\pi )^d |\mathbf{\Sigma_1}|}}\exp(-\frac{(x - \mathbf{\mu_1})^T \Sigma^{-1}_1 (x - \mathbf{\mu_1})}{2} )\gamma_1 = \frac{1}{\sqrt{(2\pi )^d |\mathbf{\Sigma_2}|}}\exp(-\frac{(x - \mathbf{\mu_2})^T \Sigma^{-1}_2 (x - \mathbf{\mu_2})}{2} ) \gamma_2 \tag{3} $$

在LDA中，继续假设了各个类别服从的正态分布的协方差矩阵是相等的。 $$ \mathbf{\Sigma_1 = \Sigma_2 = \Sigma}. $$ 基于以上假设对公式$(3)$进行化简可得(具体步骤请参考文献²)： $$ \delta(x) = 2(\Sigma^{-1}(\mu_2 - \mu_1))^T x + (\mu_1 - \mu_2)^T \Sigma^{-1} (\mu_1 - \mu_2)) + 2 \ln(\frac{\gamma_1}{\gamma_2}) = 0 $$ 上式即为两个类别之间的分界线，由于该表达式本质上为$a^Tx + b = 0$，是一条直线，所以该方法称为LDA。

在QDA中，则去除了协方差矩阵相等的假设，再对公式$(3)$进行化简可得：

$$ \delta(x) = x^T (\Sigma_1 - \Sigma_2)^{-1}x + 2(\Sigma_2^{-1}\mu_2-\Sigma_1^{-1}\mu_1 )^T x + (\mu_1^T \Sigma_1^{-1} \mu_1 - \mu_2^T\Sigma_2^{-1}\mu_2) \\ + \ln(\frac{|\Sigma_1|}{|\Sigma_2|}) + 2\ln(\frac{\gamma_2}{\gamma_1}) = 0. \tag{4} $$

上式即为两个类别之间的分界线，由于该表达式本质上为$x^TAx + b^Tx + c = 0$，是一条二次曲线，所以该方法称为QDA。

多类别情况下，假设有$k$类{$C_1, C_2, \cdots , C_k$}，对于类别$k$的后验概率为： $$ f_k(x)\gamma_k = \frac{1}{\sqrt{(2\pi )^d |\mathbf{\Sigma_k}|}}\exp(-\frac{(x - \mathbf{\mu_k})^T \Sigma^{-1}_k (x - \mathbf{\mu_k})}{2} )\gamma_k $$ 对上式区$\ln$之后，再去掉常数项后，可得类别$k$的缩放后的后验概率（scaled posterior）: $$ \delta_k(x) = -\frac{1}{2}\ln(|\Sigma_k|) - \frac{1}{2}(x-\mu_k)^T \Sigma_k^{-1} (x - \mu_k) + \ln(\gamma_k). \tag{5} $$

在判断样本$x$属于那个类别时只需要取上式值最大的即可。 $$ \hat{C}(x) = arg\max_k \delta_k(x) $$

在LDA中各个类别的协方差矩阵相等，我们将公式$(5)$进一步化简： $$ \delta_k(x) = \mu_k^T \Sigma^{-1} x - \frac{1}{2} \mu_k^T \Sigma^{-1} \mu_k + \ln(\gamma_k). $$

LDA 和 QDA中参数的求解

类的先验概率 (priors)

$$ \hat{\pi}_k = \frac{n_k}{n} $$

其中$n_k$为类别$k$的总数，$n$为总样本数

类的均值（mean of k-th class）

$$ \hat{u}_k = \frac{1}{n_k}\sum_{i=1}^{n}x_i\mathbf{I}(\mathcal{C}(x_i)=k) $$

其中$\mathbf{I}(\cdot)$为指示函数。

类的协方差（the covariance matrix of the k-th class）

$$ \mathbb{R}^{d \times d} \ni \hat{\Sigma}_k = \frac{1}{n_k} \sum_{i=1}^n(x_i-\hat{u}_k)(x_i-\hat{u}_k)^T\mathbb{I}(\mathcal{C}(x_i) = k) $$

或者使用无偏差的表达： $$ \mathbb{R}^{d \times d} \ni \hat{\Sigma}_k = \frac{1}{n_k - 1} \sum_{i=1}^n(x_i-\hat{u}_k)(x_i-\hat{u}_k)^T\mathbb{I}(\mathcal{C}(x_i) = k) $$

在 LDA, 我们假定协方差矩阵相等所以： $$ \hat{\Sigma} = \frac{\sum_{k=1}^{|\mathcal{C}|} n_k \hat{\Sigma}_k} {n} $$

MPI 实现

分别在计算先验概率、均值和协方差过程都进行了并行的计算，最后结果在master process 处获得。

参考

[1] The elements of statistical learning

[2] Linear and Quadratic Discriminant Analysis: Tutorial