Regression

线性回归

线性回归模型如下： $$ \hat{y} = \omega_0 x_0 + \cdots + \omega_m x_m + bias $$ 其中$m$为样本的特征数目。

其目标函数为最小化以下函数： $$ Cost(\hat{y}, y) = \frac{1}{2N}\sum_{j-1}^{N}||\hat{y}_j - y_j||^2 $$ 通过求导可得： $$ \frac{\partial Cost}{\partial \omega_i} = \frac{1}{N}\sum_{j=1}^{N} (\hat{y}_j - y_j) x_i^j $$ 其中$x_i^j$代表第$j$个样本的第$i$个特征值, N为训练的样本总数。

从概率论的角度： Least Square 的解析解可以用 Gaussian 分布以及最大似然估计求得

岭回归 (ridge regression)

该方法通过对模型权重进行了惩罚。其目标函数为： $$ Cost(\hat{y}, y) = \frac{1}{2N}\sum_{j-1}^{N}||\hat{y}_j - y_j||^2 + \lambda \sum_i^{m}||w_i||^2_2 $$ 其中$\lambda$为惩罚系数。需要注意此处对于$bias$没有进行惩罚。

通过求导可得： $$ \frac{\partial Cost}{\partial \omega_i} = \frac{1}{N}\sum_{j=1}^{N} (\hat{y}_j - y_j) x_i^j + 2 \lambda w_i $$

从概率论的角度： Ridge 回归可以用 Gaussian 分布和最大后验估计解释

Lasso regression

该方法通过对模型权重进行了惩罚。其目标函数为： $$ Cost(\hat{y}, y) = \frac{1}{2N}\sum_{j-1}^{N}||\hat{y}_j - y_j||^2 + \lambda \sum_i^{m}||w_i||_1 $$ 其中$\lambda$为惩罚系数。需要注意此处对于$bias$没有进行惩罚。

通过求导可得：

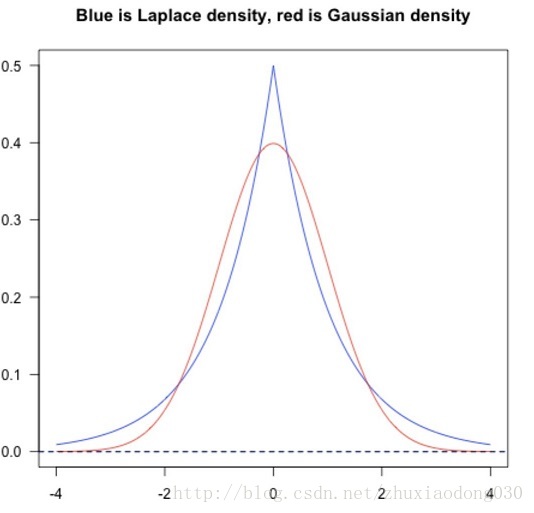
$$ \frac{\partial Cost}{\partial \omega_i} = \left\{ \begin{array}{rl} \frac{1}{N}\sum_{j=1}^{N} (\hat{y}_j - y_j) x_i^j + \lambda & if \ w_i >= 0 \\ \frac{1}{N}\sum_{j=1}^{N} (\hat{y}_j - y_j) x_i^j - \lambda & if \ w_i < 0 \end{array}\right. $$

从概率论的角度：LASSO 回归可以用 Laplace 分布和最大后验估计解释。从贝叶斯角度，正则项等价于引入参数的先验概率分布。常见的L1/L2正则，分别等价于引入先验信息：参数符合拉普拉斯分布/高斯分布。

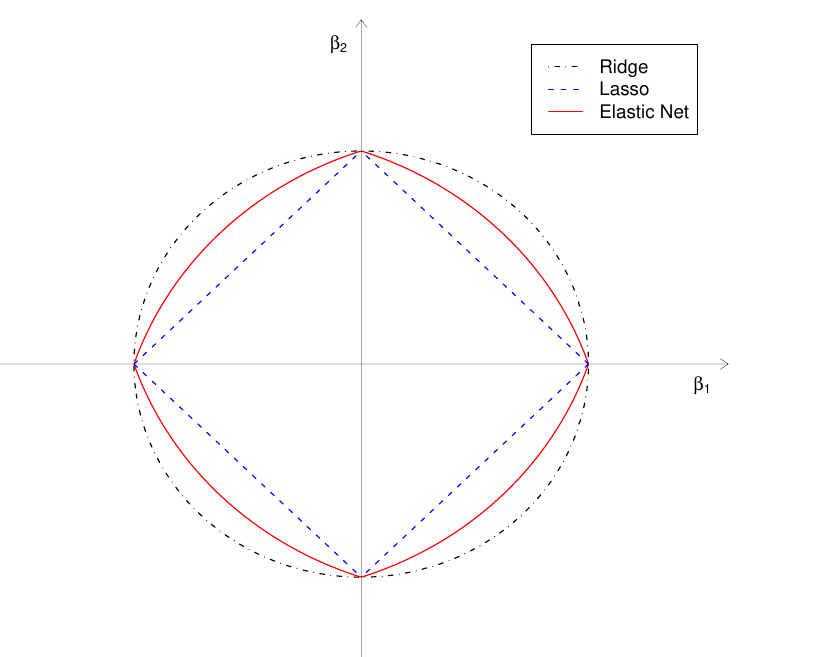
Elastic Net

Elastic net回归将ridge和lasso回归结合了起来，它同时使用了$L_1$和$L_2$正则项: $$ Cost(X, Y) = \frac{1}{2N} \sum_{i=1}^N ||\hat{y}_j - y_j||^2 + \lambda_1 \sum_{j=1}^J |\omega_j| + \lambda_2 \sum_{j=1}^J \omega_j^2. $$ 其中$\lambda_1$和$\lambda_2$分别为$L_1$和$L_2$正则项的惩罚系数，此处对于$bias$没有进行惩罚。

通过求导可得：

$$ \frac{\partial Cost}{\partial \omega_i} = \left\{ \begin{array}{rl} \frac{1}{N}\sum_{j=1}^{N} (\hat{y}_j - y_j) x_i^j + \lambda_1 + 2\lambda_2 \omega_i & if \ w_i >= 0 \\ \frac{1}{N}\sum_{j=1}^{N} (\hat{y}_j - y_j) x_i^j - \lambda_1 + 2\lambda_2 \omega_i & if \ w_i < 0 \end{array}\right. $$

Polynomial Regression

多项式回归（polynomial regression）模型的形式如下： $$ \mathbf{y = Xb + e} $$ 展开表示为：

$$ \left [ \begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n \end{array} \right ] = \left [ \begin{array}{ccccc} 1 & x_1 & x_1^2 & \cdots & x_1^p \\ 1 & x_2 & x_2^2 & \cdots & x_2^p \\ \vdots & \vdots & \vdots& \ddots & \vdots \\ 1 & x_n & x_n^2 & \cdots & x_n^p \end{array} \right ] \left [ \begin{array}{c} b_1 \\ b_2 \\ \vdots \\ b_n \end{array} \right ] + \left [ \begin{array}{c} e_1 \\ e_2 \\ \vdots \\ e_n \end{array} \right ] $$

其中$\mathbf{e}$为误差。

一个简单的样例（特征维数为2）： $$ y = w_0 + w_1 x_1 + w_2 x_2 + w_{11}x_1^2 + w_{22}x_2^2 + w_{12}x_1x_2 + e $$

在简单的样例中特征数为2，多项式度数为2，转化后的特征数则有5个。

可知对于$(x_1 + x_2 + \cdots + x_p)^q$我们可以得到不同的项数的数目为$C_{p+q-1}^{p-1}$(等同于将q个相同的球放进p个不同的抽屉)。推广到一般的形式，假定原特征维度为$p$，多项式回归中的度数为$d$，转化后的特征的数目为： $$ \sum_{i=1}^d C_{p+i-1}^{p-1} $$

对于输入的$X$我们首先对原特征进行多项式的转换得到新的特征，之后在新得到的特征上进行线性回归即可。

Logistic Regression

在逻辑回归中，我们假定y ( y的取值为{0, 1} ) 服从伯努利分布$p(y|X, w) = Ber(y|u(x))$，其中$u(x) = sigmoid(w^TX)$

逻辑回归相关的函数：

$$ z = \omega_0 + \omega_1x_1+ \cdots + \omega_n x_n\\ \hat{y} = sigmoid(z) = \frac{1}{1+e^{-z}}\\ cost(y, \hat{y}) = -[y\ln\hat{y}+(1-y)\ln(1-\hat{y})] $$

其中{$\omega_0 \cdots \omega_n$}为模型参数，{$x_1 \cdots x_n$}为样本的特征值。

复合函数分别求导可得：

$$ \frac{\partial cost}{\partial \hat{y}}=-\frac{y}{\hat{y}}+\frac{1-y}{1-\hat{y}}\\ \frac{\partial \hat{y}}{\partial z} = \hat{y}(1-\hat{y})\\ \frac{\partial z}{\partial \omega_i} = x_i\\ $$

最终可得$cost$函数关于$\omega_i$的导数： $$ \frac{\partial cost}{\partial \omega_i} = (\hat{y} - y)x_i $$ 所以参数$\omega_i$更新公式为： $$ \omega_i = \omega_i - \alpha(\hat{y}-y)x_i $$ 其中$\alpha$为学习率。

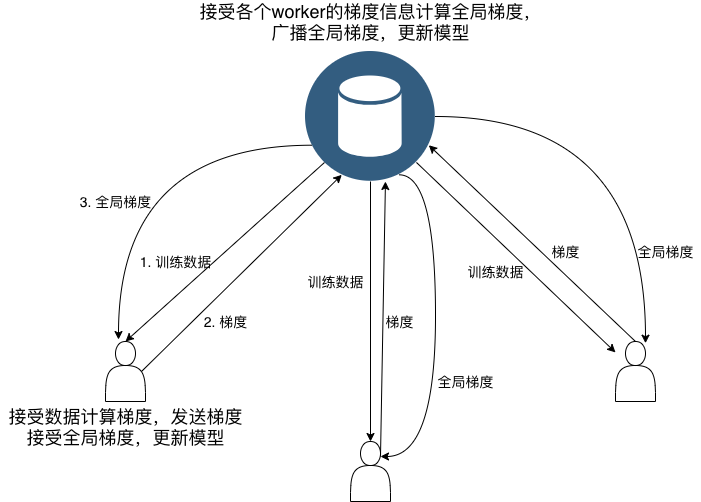
MPI 实现

参数$w_i$更新可表示为; $$ w_i = w_i - \alpha\frac{1}{N}\sum_{j=1}^{N}\nabla w_i^{j} $$ $\nabla w_i^{j}$ 代表基于样本$j$所求的$w_i$的梯度。所以我们可以在计算梯度是进行并行执行，然后由master对梯度信息进行收集和计算全局的梯度。

MPI实现策略