Robust Regression

评价标准

Breakdown point 和 efficiency是两种传统的衡量不同健壮（robust）方法的指标；

Breakdown point: 用来衡量方法在异常点（outliers）拥有多少比例的情况下会出现输出无限的值，即如果$[N\alpha]$个数据点$\rightarrow \infty$,该方法会输出$\infty$.
Efficiency: 指的在数据集内正常无异常点的情况下，该方法和一般的最小二乘方法（ordinary least squares）在效率上的比例

举个例子，对于求平均值$\bar{x}_n$:

$$ \begin{array}{ll} \bar{x}_n &= \frac{1}{n}\sum_{i=1}^{n} x_i \\ & = \frac{n-1}{n} \bar{x}_{n-1} + \frac{1}{n}x_n \\ \end{array} $$

求平均值的时候，如果异常值$x_n$足够的大，将会导致输出结果错误。而对于求中位数，则可以允许错误的数据达到50%。一般来说breakdown不能超过50%.

异常值

异常值出现在Y的维度上
异常值出现在X的维度上（leverage points）
异常值出现在X，Y的维度上

M-Estimation

线性的最小二乘法（linear least-squares）在数据不正常，拥有异常值的情况下很可能表现非常的差。由此人们想出了robust regression的方法，能对异常值进行处理。最普遍的robust regression的方法为M-estimation.

考虑以下线性模型:

$$ \hat{y}_i = a + b_1x_{i1} + b_2 x_{i2} + \cdots + b_k x_{ik} = \mathbf{x_i b} $$

误差为：

$$ e_i = y_i - \hat{y}_i $$

在M-estimation中求解$\mathbf{b}$是通过最小化一个特定的目标函数($\rho()$)

$$ \sum_{i=1}^n \rho(e_i) = \sum_{i=1}^n \rho (y_i - \mathbf{x_i b}) \tag{1} $$ 其中函数$\rho$决定了每个样本残差对于总目标的贡献权重。

一个合理的函数$\rho$需要满足以下条件：

非负 $\rho(e) \geq 0$
$\rho(0) = 0$
$\rho(e) = \rho(-e)$
在$|e_i|$单调, $\rho(e_1)\geq \rho(e_2)$, $|e_1| \geq |e_2|$

比如，最小二乘的$\rho(e_i) = e^2_i$就满足以上要求。

我们令$\psi()$为$\rho()$函数的导函数（一般称$\psi()$为影响曲线(influence curve)）。所以我们可以将公式$(1)$进行求导可得： $$ \sum_{i=1}^n \psi(y_i - \mathbf{x_i b})\mathbf{x_i} = 0 $$ 令权重函数(weight function)为$w(e)=\psi(e)/e$，和令$w_i = w(e_i)$.所以上式可以表示成： $$ \sum_{i=1}^n w_i(y_i - \mathbf{x_i b})\mathbf{x_i} = 0 \tag{2} $$ 公式$(2)$可以看成是加了权重的最小二乘问题 $$ \sum w_i^2 e_i^2 $$

由上式可看出，权重的值是由误差$e$决定，误差$e$又是由$\mathbf{b}$决定，而模型参数$\mathbf{b}$又是由权重决定。所以采用迭代的方法进行求解：

选择初始的模型参数值$\mathbf{b}^{(0)}$（比如由最小二乘法得来）
在每次迭代$t$中，计算误差值$e_i^{(t-1)}$，求解相关的权重$w_i^{(t-1)}=w[e_i^{t-1}]$
求解新的模型参数值$\mathbf{b^{(t)}}$ $$ b^{(t)} = [X^T W^{(t-1)} X]^{-1}X^T W^{t-1}y $$ 其中$W^{(t-1)}$是对角矩阵$diag${$w_i^{(t-1)}$}, $X$是{n_sample, n_features}的矩阵, y是列向量。以上求解过程重复2,3步骤直至模型参数$\mathbf{b}$收敛。总的看来，整个求解过程就是在每次迭代中我们都是求解一个带权重的最小二乘问题, 而该权重的得来是由上一次迭代中的误差决定。

M-estimation方法适用于异常值在Y的维度上，但是不适合异常值发生在X的维度上(leverage points)

目标函数($\rho$函数)

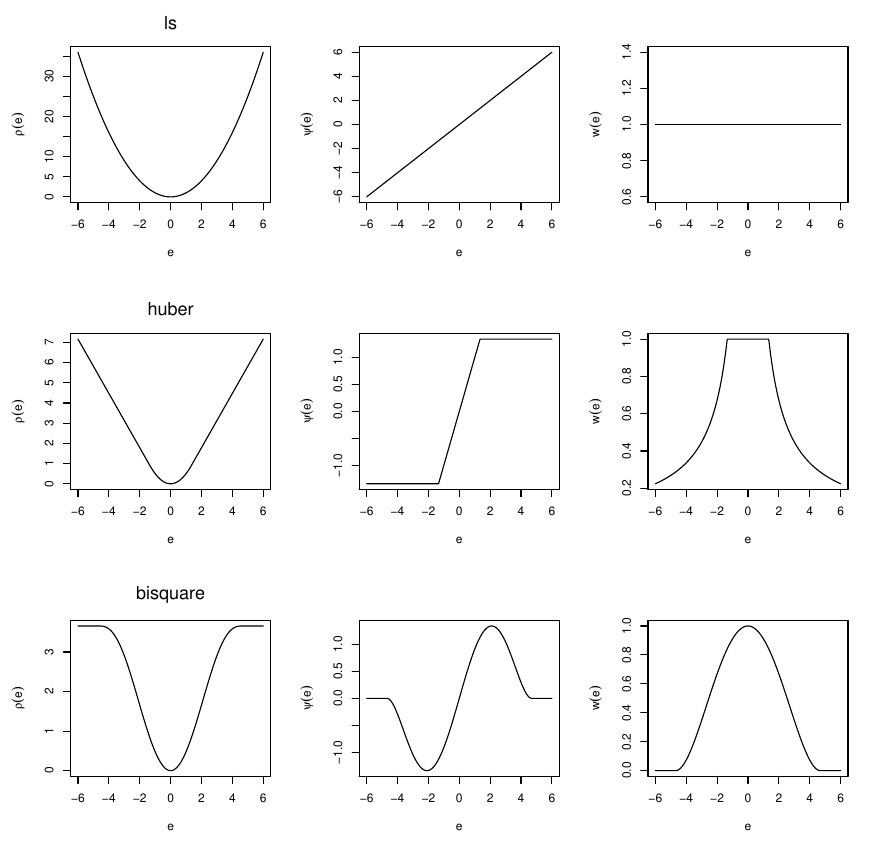
常见的三种$\rho$函数：这三种$\rho$函数的图像如下：

S-estimation

S-estimation的目标是最小化以下值： $$ \min_{\hat{\theta}} s(r_1(\theta), \cdots, r_n(\theta)) $$ 其中$s(r_1(\theta), \cdots, r_n(\theta)$定义为以下方程的解： $$ \frac{1}{n}\sum_{i=1}^n \rho (\frac{r_i}{s}) = K. $$ 通常$K$取值为$E_{\Phi}[\rho]$，其中$\Phi$为标准正太分布。

最终最小化的目标值（final scale estimator）是： $$ \hat{\rho} = s(r_1(\hat{\theta}), \cdots, r_n(\hat{\theta})). $$

本方法使用的函数$\rho()$需要满足以下条件：

$\rho$是对称的且连续可导，$\rho(0) = 0$
存在$c > 0$ 使得函数$\rho$在$[0, c]$是严格的递增，在$[c, \infty)$为常数。

本方法的优点是可以获得很高的breakdown point和在正常数据的情况下实现高效率。

$\rho$函数

$$ \rho(x) = \left \{ \begin{array}{ll} \frac{x^2}{2} - \frac{x^4}{2c^2} + \frac{x^6}{6c^4} & \ \ for \ |x| \leq c \\ \frac{c^2}{6} & \ \ for \ |x| > c. \end{array} \right. $$

以上函数的导函数为(称为Tukey's biweight function)：

$$ \psi(x) = \left \{ \begin{array}{ll} x(1-(\frac{x}{c})^2)^2 & \ \ for \ |x| \leq c \\ 0 & \ \ for \ |x| > c. \end{array} \right. $$

MM-estimates

给定n个样本的数据集$\mathbf{u} = (u_1, u_2, \cdots, u_n)$，数值估计(scale estimate)$s(\mathbf{u})$）（简写为s）定义为以下方程的解： $$ \frac{1}{n} \sum_{i=1}^n \rho (u_i / s) = b. $$ 其中$b$可能定义为$E_{\psi}(\rho(u)) = b$, $\psi$代表了标准正态分布。