Methods
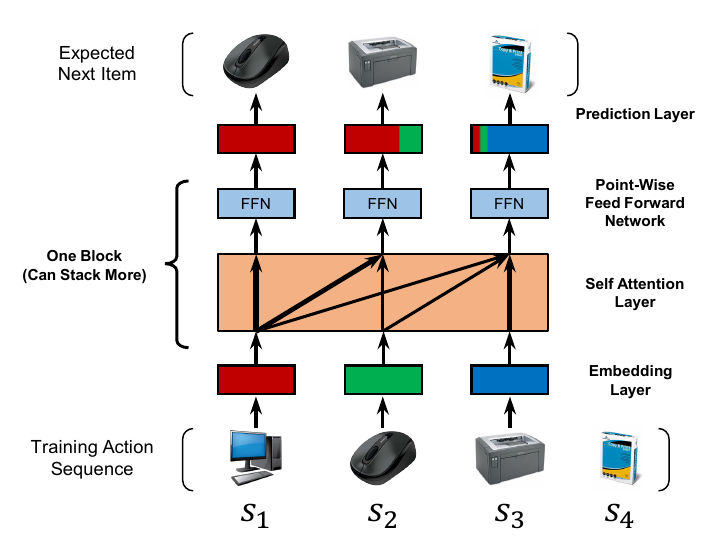
Embedding Layer
In embedding layer, we transform the training sequence $((S_1^u, S_2^u, \cdots, S^u_{|S^U|-1})$ into a fixed-length sequence $s = (s_1, s_2, \cdots, s_n)$, where n represent the maximum length that the model can handle. $E \in R^{n \times d}$ is the input embedding matrix. To add the positions information, we inject a learnable position embedding $P \in R^{n \times d}$ $$ \hat{\mathbf{E}} = \mathbf{E + P} $$
Self-Attention Block
The scaled dot-product attention is defined as; $$ Attention(\mathbf{Q, K, V}) = softmax(\frac{\mathbf{QK}^T}{\sqrt{d}})\mathbf{V}. $$ where Q represents the queries, K the keys and V the values.
First we convert the input $\hat{E}$ to three matrix, then feeds into an attention layer: $$ S = SA{\hat{\mathbf{E}}} = Attention(\mathbf{\hat{E}W^Q, \hat{E}W^K, \hat{E}W^V}) $$ where the projection matrices $W^Q, W^K, W^V \in R^{d \times d}$ are learnable.
The self-attention is able to aggregate all previous item's embeddings with adaptive weights, but it is stills a linear model. To endow the model with nonlinearity, we apply a point-wish two-layer fead-forward network to all $S_i$ identically (sharing parameters): $$ F_i = FFN(S_i) = ReLU(S_iW^1 + b^1) W^2 + b^2 $$ where $W^1, W^2 \in R^{d \times d}$ are matrices and $b^1, b^2$ are d dimensional vectors.
Stacking Self-Attention Blocks
We stack the self-attention block as follow:
To overcome the problems
- the increased model capacity leads to overfitting;
- the training process becomes unstable (due to vanishing gradients etc.);
- models with more parameters often require more training time.
We perform the following operations: $$ g'(x) = x + Dropout(g(LayerNorm(x))) $$ where g(x) represents the self attention layer or the fed-forward network.
Prediction Layer
We adopt an MF layer to predict the relevance of items i: $$ r_{i, t} = F_t^b N_i^T $$ where $r_{i, t}$ is the relevance of item i being the next item given the first t items, and $N \in R^{|I| \times d}$ is an item embedding matrix.
To reduce the model size and alleviate overfitting, we can use a single item embedding $M$; $$ r_{i, t} = F_t^b M_i^T $$ where the $M$ is the embedding matrix we used before. Empirically, using a shared item embedding significantly improves the performance of the model.